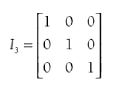Sendo dadas as matrizes A = (aij) e B = (bij), quadradas de ordem 2, com aij = 3i + 4j e bij = – 2i – j. Considerando C = A + B, a matriz C será:
Como o determinante de M é não nulo, a matriz M é invertível. Se sua inversa é da forma 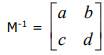 , então, o resultado da expressão numérica 5a + 4b + 3c + 2d é
, então, o resultado da expressão numérica 5a + 4b + 3c + 2d é
Sendo as matrizes A e B, qual o valor de 3A - B + 10?
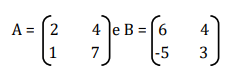
Julgue o item que se segue, relativo a matrizes e sistemas lineares.
Se 0 é a matriz nula n × n, se I é a matriz identidade n × n, e se P é uma matriz n × n tal que P2 + 2P + I = 0, então P é inversível.
Dada a matriz A=(aij)2x2 tal que aij = 2i – j, é correto afirmar que o elemento a12 da matriz, é igual a:
Dadas a matriz 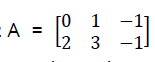
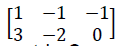
Dada a matriz A = 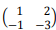 ,seja a matriz B dada por B = A-1, então a matriz B é igual a;
,seja a matriz B dada por B = A-1, então a matriz B é igual a;
Julgue o item que se segue, relativo a matrizes e sistemas lineares.
Se
a é um número real e se o determinante da matriz 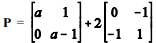
Sejam A uma matriz quadrada de ordem 2 e B uma matriz quadrada de ordem 3, tais que detA . detB = 1. O valor de det(3A) . det(2B) é
Julgue o item que se segue, relativo a matrizes e sistemas lineares.
Se P for uma matriz simétrica, então P será inversível.
A matriz a seguir é conhecida por:
Analise as quatro afirmações abaixo sobre uma matriz quadrada do tipo N x N:
I. O número de elementos fora da diagonal principal será N · (N -1).
II. Uma matriz N x N só pode ser multiplicada por uma outra matriz N x N.
III. O produto de uma matriz N x N por qualquer outra matriz sempre irá resultar em uma outra matriz quadrada.
IV. Toda matriz quadrada N x N é inversível.
Assinale a alternativa correta:
Em uma sala de aula, entre alunos e alunas, há 36 pessoas.
Se, em determinado dia, seis das alunas faltarem às aulas e
todos os alunos se fizerem presentes, então, nesse dia, a
quantidade de alunos será o dobro da de alunas. Um
problema que se coloca é determinar quantos alunos e
quantas alunas pertencem a essa sala.
A respeito dessa situação hipotética, julgue os itens
subsecutivos.
O problema enunciado pode ser formalizado por uma equação matricial da forma AX = B, em que A é uma matriz quadrada 2 × 2, X e B são matrizes-colunas 2 × 1 e o determinante da matriz A é diferente de zero.
Um projeto de iniciação científica está aberto à três áreas de conhecimento, nos quais um pesquisador deverá atuar em 2 destes projetos, não obrigatoriamente distintos, porém: um no primeiro semestre e um no segundo semestre. A matriz a seguir representa o esquema de mudança ou aprofundamento de projetos, concluído, entre os semestres.
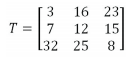
Sabe-se que Tij representa o número de pesquisadores que mudaram do projeto i para o j, quando i≠j e Tij representa o número de pesquisadores que preferiram aprofundar no mesmo tema e não mudaram de projeto, quando i=j. Neste caso, determine o número total de pesquisadores matriculados nos três projetos.
Considere que nenhum pesquisador abandonou o programa de iniciação científica, bem como nenhum outro ingressou neste programa.
Dadas a matriz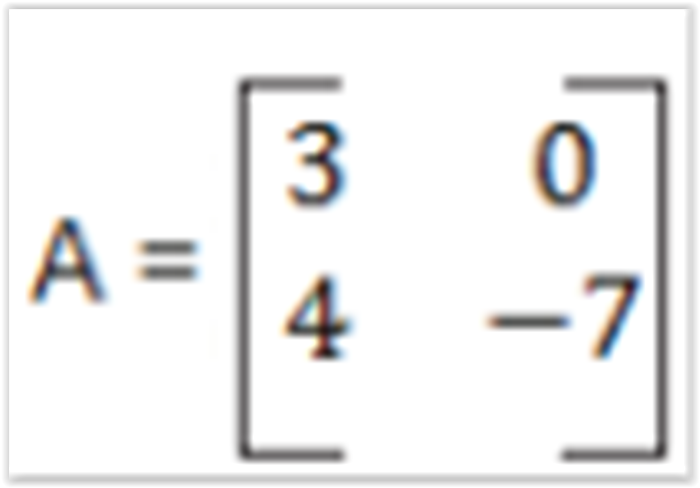
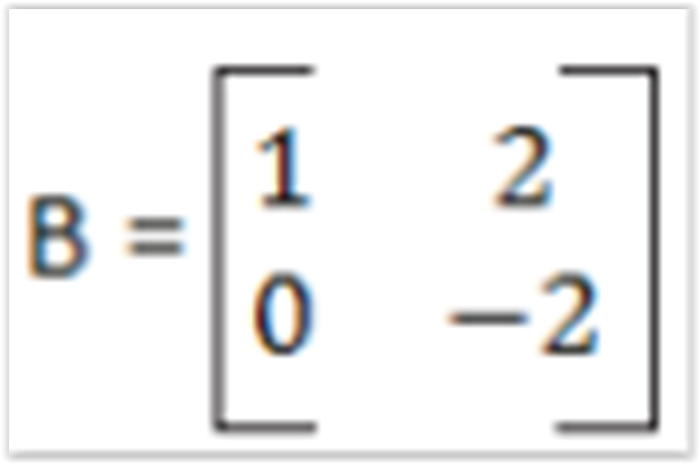
assinale a alternativa que apresenta a matriz C que
representa a subtração da matriz A e B, ou seja, C = A - B.