Partindo do estudo da matriz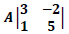 
encontra-se a matriz 
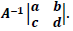Com os valores obtidos em
Dadas as matrizes:
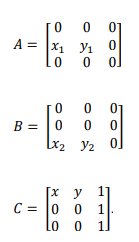
O determinante de D = A + B + C é:
Considere os pontos de coordenadas (x,y) associados à matriz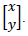 
Na figura representada no plano cartesiano da figura 1 pretende-se fazer uma rotação em torno da origem deixando-a como na figura 2. Para isso deve-se multiplicar uma matriz M pela matriz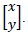 
A matriz M é:
Um produtor de queijos resolveu abrir duas lojas para revenda de sua produção: a loja A no estado de São Paulo e a B em Minas Gerais. Sabe-se que o mesmo produz quatro tipos de queijo (1, 2, 3 e 4). As matrizes abaixo mostram a venda de cada tipo de queijo nos dois primeiros meses da loja onde cada elemento aij, na matriz A, e bij, na matriz B, indicam o tipo de queijo i vendido no mês j de venda.
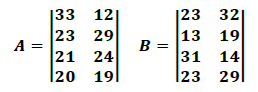
Assinale a alternativa que corresponde a uma afirmação verdadeira.
Considere a matriz real quadrada A de ordem 3, onde seus elementos são definidos por aij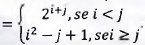 
A soma dos elementos que compõem a diagonal principal é
O estudo das matrizes tem muitas aplicações na computação gráfica. É através de operações com matrizes que um programa gráfico altera a posição dos pontos que compõem uma imagem, fazendo-a girar, mudar de posição ou de escala. Na computação grafia, essas operações recebem o nome de transformações geométricas. Por exemplo, uma rotação de 0 graus de um ponto P = (x ,y ), em torno da origem no sentido anti-horário é feita a partir do produto da matriz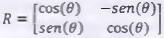 
de rotação com a matriz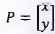 
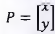, que resulta em uma matriz 
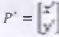, a qual indica a nova posição do ponto após a rotação: P¹ = R . P
A nova posição do ponto P = (1,2) apos uma rotação de 90 graus no sentido anti-horário, tomo da origem, é:
Durante um campeonato de basquete, a comissão técnica de um time anotou a pontuação de alguns jogadores na matriz a seguir:
O elemento aij dessa matriz representa o número de pontos marcados na partida i pelo jogador j. Qual jogador marcou mais pontos nesse campeonato?
Sendo as matrizes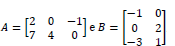 
, é correto afirmar que o produto matricial é igual a:
O termo a21 da matriz A = (aij)2×2 dada por aij = 3i – j é igual a:
Se P é uma matriz 2x2 tal que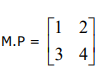 
, então, o determinante da matriz P é igual a
Considere a matriz quadrada A, de ordem 2, definida por:
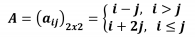
O determinante dessa matriz A será igual a
Dado uma matriz A4x4 =(aij) tal que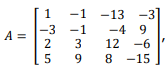 
então é possível afirmar que:
Sejam A e B duas matrizes quadradas 2x2, tal que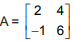 
, e A.B = I, onde I é a matriz identidade 2x2.
Assim, a soma dos elementos da matriz B é igual a
Assinale a alternativa que apresenta os valores de x e y, respectivamente, para que as matrizes A e B sejam inversas.
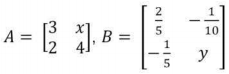
Se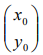 
é solução da equação matricial 
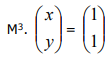, então, o valor da soma x0 + y0 é igual a
