Giulia desafiou sua irmã a descobrir quantos números naturais de apenas algarismos impares distintos estão compreendidos no intervalo de 100 a 800. A resposta correta para o desafio será?
O princípio fundamental da contagem pode ser usado em grande parte dos problemas relacionados com contagem. Entretanto, em algumas situações seu uso torna a resolução muito trabalhosa. Desta maneira, usamos algumas técnicas para resolver problemas com determinadas características. Basicamente há três tipos de agrupamentos: arranjos, combinações e permutações. Com base nessa informação relacione as colunas abaixo: 1) Arranjos: 2) Combinações: 3) Permutações: ( ) os agrupamentos dos elementos dependem da ordem e da natureza dos mesmos. ( )são agrupamentos ordenados, onde o número de elementos (n) do agrupamento é igual ao número de elementos disponíveis. ( ) são subconjuntos em que a ordem dos elementos não é importante, entretanto, são caracterizadas pela natureza dos mesmos. Assinale a alternativa CORRETA:
A senha de uma conta bancária, é constituída de três letras e três números. Sabendo que as letras são escolhidas dentre as 26 letras do alfabeto e os números entre nove algarismos de 1 a 9. Quantas senhas podem ser formadas usando-se três vogais e três números ímpares?
De quantas maneiras 6 peixes podem ser agrupados em 3 três aquários que estão dispostos lado a lado, em um balcão, de modo que peixes da mesma espécie fiquem juntos e sabendo-se que há exatamente dois peixes de cada espécie?
No Porto de Itaqui, 16 contêineres serão embarcados em 2 navios: cada navio deverá levar exatamente 8 desses contêineres. Do total de contêineres, 8 estão carregados com frango congelado, 3, com carne bovina congelada e 5, com soja.
A partir dessas informações, julgue o item que se segue.
A quantidade de maneiras distintas de se embarcarem, no primeiro navio, 4 contêineres de frango congelado e 4 de soja e, no segundo navio, 4 contêineres de frango congelado, 1 de soja e 3 de carne bovina congelada é superior a 330.
A turma do Rafael tem doze alunos, contando com o Rafael. De quantas maneiras podemos formar trios de modo que Rafael sempre participe?
Em uma lanchonete, o açaí pode ser acompanhado por vários adicionais e é vendido em três tamanhos diferentes: pequeno, médio e grande. O cliente escolhe o tamanho e, em seguida, escolhe seus adicionais preferidos, de acordo com o tamanho. Para o tamanho pequeno, pode escolher até dois adicionais; para o médio, até três adicionais e, para o grande, até quatro adicionais. Considerando que há 10 tipos diferentes de adicionais, de quantos modos diferentes um cliente pode pedir um açaí com o máximo de adicionais permitidos?
Considere um conjunto de 10 empresas, denominadas A, B, C, D, E, F, G, H, I e J. Um analista precisa escolher quatro dessas empresas para distribuir quatro serviços diferentes, um para cada uma escolhida. Após uma análise técnica, decidiu que exatamente duas das três primeiras empresas — A, B e C — deveriam fazer quaisquer dois serviços dentre os quatro disponíveis. Os outros dois serviços que sobrassem seriam distribuídos entre duas das sete outras empresas restantes. Nessas condições, o número de possibilidades diferentes para essa distribuição de serviços é igual a
O Corpo de Bombeiros de Minas Gerais recebeu 25 pedidos de avaliação da necessidade de corte de 25 árvores em diferentes bairros da capital. Sabe-se que esses pedidos eram oriundos de 5 regionais distintas, explicitadas na tabela a seguir.
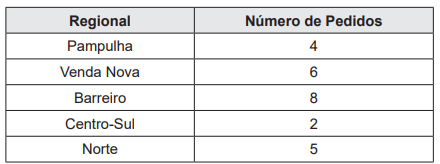
Para otimizar o trabalho, os bombeiros envolvidos devem criar uma rota, em que todos os 25 pedidos devem ser atendidos. A rota constituída deve seguir estes critérios:
– os bombeiros só seguiriam para outra regional quando concluíssem o trabalho da regional que estavam atendendo, e assim por diante;
– em uma mesma regional, a ordem entre as árvores avaliadas poderia ser escolhida livremente;
– a ordem entre as regionais poderia ser escolhida livremente, para constituir a rota de atendimento.
Quantas rotas de atendimento diferentes podem ser elaboradas pelos bombeiros envolvidos?
Considere todas as senhas formadas por três vogais maiúsculas. São exemplos dessas senhas: EEE, OIA e UAU.
Dentre todas as senhas desse tipo, escolhendo ao acaso uma delas, a probabilidade de que ela tenha duas letras iguais e uma diferente é de
A senha de determinado computador é um número de quatro algarismos distintos formado por elementos do conjunto {1, 2, 4, 5, 8, 9}. Nesse caso, o número de senhas diferentes possíveis é igual a
Dos 10 administradores do CFO, 4 serão escolhidos para compor a comissão de licitação de compras diversas. A comissão terá um presidente, um vice-presidente, um secretário e um auditor, não podendo haver acúmulo de cargos. Jonas é um desses 10 administradores.
Com base nesse caso hipotético, julgue o item que se segue.
Considere-se que tenham sido listadas todas as possíveis comissões e que cada uma delas tenha sido escrita em um pedaço de papel, dobrado e colocado em uma urna para uma escolha aleatória. Nesse caso, a probabilidade de se escolher uma comissão em que Jonas não ocupe nenhum dos 4 cargos é superior a 65%.
Matheus anotou um código binário, utilizando apenas 0 e 1, em uma matriz 4 x 4 para formar uma senha. Quando precisou do código, percebeu que seu cachorro havia rasgado o papel em que anotara e conseguiu achar apenas um pedaço do papel.
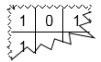
Como Matheus sabia que o código era formado por 7 dígitos 1's e 9 dígitos 0's, ele resolveu testar todas as possibilidades. Qual o número máximo de tentativas que ele deve fazer para descobrir o código que estava escrito anteriormente, se no pedaço que ele achou estavam escritos 3 dígitos 1's e um dígito 0?
Os colaboradores de uma empresa são identificados com uma senha formada por três algarismos sendo exatamente dois destes algarismos iguais. Por exemplo: (003) e (030) são senhas diferentes. O número de senhas que podem ser criadas é
Uma sala de aula possui 5 portas. Quantas maneiras diferentes ela pode ser aberta, sendo que no mínimo 2 portas devem ficar abertas?

