Considere o plenário de um tribunal superior composto por 11
ministros, sendo duas mulheres e nove homens. Uma turma com
cinco integrantes será escolhida ao acaso para apreciação de
determinados processos.
A probabilidade de que tal turma seja mista, do ponto de vista do
gênero, é igual a:
Numa localidade que conta apenas com duas varas de justiça e onde os processos são distribuídos de forma aleatória, sabe-se que o juiz “A” condena os réus com probabilidade de 0,45 e o juiz “B” absolve com probabilidade 0,85. Logo, a probabilidade de que um réu qualquer seja absolvido é de:
Considere a variável aleatória X, uniforme entre 0 e 1, uma amostra aleatória simples de tamanho n=3 e a estatística de ordem do máximo (=Y). Então a função de densidade de Y é dada por:
Seja X = número de anos de condenação e Y = nível de renda do
condenado (mil reais). São fornecidas ainda as seguintes
informações:
Var(X ) = 25; Var (Y ) = 16 e Var (X+Y) = 21
Assim sendo, a correlação (Pearson) entre X e Y é igual a:
Para estimar a média populacional μ é sugerido o estimador
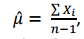
onde xié o indivíduo de ordem i de uma amostra
aleatória simples extraída daquela população.
Então, é correto afirmar que:
Sobre a realização de testes de razão de verossimilhança, a partir de uma AAS de tamanho n, é correto afirmar que:
Considere a tabela resumo a seguir contendo as estimativas dos
parâmetros de uma regressão linear simples e dos respectivos
erros padrão estimados, com uma amostra de tamanho n = 52:

A respeito da inferência sobre os parâmetros, é correto afirmar
que:
A estimativa de máxima verossimilhança para a variância populacional é igual a 2,1
A sequência a seguir mostra o número de gols marcados pelo funcionário Ronaldão nos nove últimos jogos disputados pelo time da empresa onde ele trabalha:
2, 3, 1, 3, 0, 2, 0, 3, 1.
Sobre a média, a mediana e a moda desses valores é verdade que:
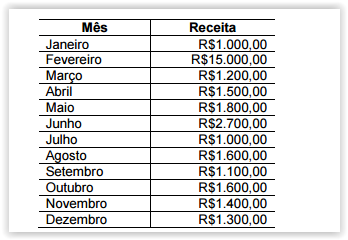
Uma Sociedade Empresária obteve uma receita total, no ano de 2014, no valor
de R$31.200,00, distribuída mensalmente como segue:
Analisando-se os dados e calculando-se as medidas de tendência central,
pode-se afirmar que a mediana é de:
Uma população é formada por números estritamente positivos apresentando uma distribuição unimodal e caracterizando uma curva de frequência assimétrica à direita. Então, é correto afirmar com relação a esta distribuição que
Conclui-se que, com a utilização do Teorema de Tchebichev, uma variável aleatória X com média igual a 50 apresenta uma probabilidade mínima de 75% de X pertencer ao intervalo (45 , 55). A variância de X é
Acredita-se que a probabilidade de ocorrência de um evento em uma experiência é de 80%. Uma série de 5 experiências é realizada e decide-se aceitar a hipótese da probabilidade de ocorrência do evento ser 80% se ele ocorrer, pelo menos, em 4 destas experiências. Sendo verdadeira a hipótese de que a probabilidade de ocorrência do evento é de fato 80%, então a probabilidade desta hipótese ser rejeitada na realização da série de 5 experiências é
Um modelo de regressão linear múltipla, com intercepto, consiste em uma variável dependente, 4 variáveis explicativas e o erro aleatório com as respectivas hipóteses do modelo de regressão linear múltipla. Com base em 21 observações e utilizando o método dos mínimos quadrados obtiveram-se as estimativas dos parâmetros deste modelo. Dado que a variação total foi igual a 100 e a estimativa da variância do modelo foi igual a 1,25, então o valor da estatística F (F calculado) utilizado para testar a eXistência da regressão, a um determinado nível de significância, foi igual a
Os processos que chegaram a um determinado Tribunal Regional Eleitoral, no primeiro semestre de 2014, foram encaminhados para o parecer de dois analistas: M e N, sendo que M e N analisaram 60% e 40% dos processos, respectivamente. Sabe-se também que 10% e 5% dos processos analisados por M e N, respectivamente, foram rejeitados por problemas na documentação. Se um processo for escolhido ao acaso, dentre todos os recebidos no primeiro semestre de 2014, a probabilidade de que tenha sido encaminhado para M, sabendo-se que foi rejeitado, é, em %, igual a