Com o objetivo de se estimar a idade média, μ, em anos, de ingresso no primeiro emprego formal de jovens de determinada
comunidade, selecionou–se uma amostra aleatória de 100 jovens da população de jovens que já haviam ingressado no mercado
de trabalho formal. Os resultados obtidos encontram–se na tabela de distribuição de frequências apresentada a seguir:
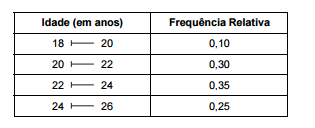
Considere:
I. Que a população de onde a amostra foi retirada é infinita e tem distribuição normal com desvio padrão igual a 1 ano.
II. Para a estimativa pontual de μ a média aritmética das 100 idades apresentadas, calculada considerando que todos os
valores incluídos num intervalo de classe são coincidentes com o ponto médio do intervalo.
Nessas condições, o intervalo de confiança para μ, em anos, com coeficiente de confiança igual a 77%, baseado nessa amostra,
é dado por
A senha requerida para ligar um computador é formada pelas mesmas 8 letras da palavra TERESINA, com as vogais ocupando as 4 primeiras posições e, as consoantes, as 4 últimas. Conhecendo apenas essas informações, uma pessoa que deseja usar o computador vai digitando todas as possíveis senhas, até acertar a correta. Se essa pessoa nunca digitar a mesma senha mais de uma vez, conseguirá descobrir a senha correta em, no máximo,
Seja uma representação gráfica de dados de acordo com o desenho esquemático abaixo (box-plot) que foi preparado para
comparar todos os salários dos funcionários do sexo masculino (Grupo I) com todos os salários dos funcionários do sexo
feminino (Grupo II) lotados em um órgão público.
este desenho esquemático
Um levantamento realizado em duas empresas X e Y com todos os seus empregados forneceu o seguinte resultado com relação
aos salários destes empregados:
Considerando o conjunto de todos os empregados das duas empresas X e Y obtém-se que a média dos salários de todos estes
empregados é, em R$, igual a
A probabilidade de ocorrência de um evento em uma determinada experiência é igual a p. Considerando as hipóteses
determina-se que H0 será aceita se e somente se o evento ocorrer
em pelo menos 4 vezes em uma série de 5 experiências executadas. A potência deste teste é igual a
Atenção: Para responder às questões de números 37 e 38 considere o modelo de regressão linear simples correspondente à equação Y i = α + βXi + ϵi (i = 1, 2, 3, ...) que é utilizado por uma empresa para prever o seu faturamento bruto (Y), em milhões de reais, em função do dispêndio com material promocional (X), também em milhões de reais. Os parâmetros α e β são desconhecidos, ϵi corresponde ao erro aleatório com as respectivas hipóteses do modelo de regressão linear simples e i refere-se à i-ésima observação das variáveis. As estimativas de α e β (a e b, respectivamente) foram obtidas pelo método dos mínimos quadrados, com base em 10 pares de observações (Xi , Yi ).
Pelo quadro de análise de variância correspondente e considerando que 
Suponha que ao realizar um experimento, ocorra o evento A com probabilidade p ou não ocorra A com probabilidade (1 - p). Repete-se o experimento de forma independente até que o evento A ocorra pela primeira vez. Seja X a variável aleatória que representa o número de repetições do experimento até que A ocorra pela primeira vez. Se a média de X for igual a duas vezes variância de X, a probabilidade de X ser igual a 4 é igual a
Atenção: Para responder às questões de números 49 a 53 utilize, dentre as informações dadas a seguir, as que julgar apropriadas.
Se Z tem distribuição normal padrão, então: P(Z < 0,5) = 0,591; P(Z < 1) = 0,841; P(Z < 1,15) = 0,8951; P(Z < 1,17) = 0,879; P(Z < 1,2) = 0,885; P(Z < 1,4) = 0,919; P(Z < 1,64) = 0,95; P(Z < 2) = 0,977; P(Z < 2,06) = 0,98; P(Z < 2,4) = 0,997.
-------------------
Instrução: O enunciado a seguir refere-se às questões de números 49 a 51. Considere que X é a variável aleatória, que representa as idades, em anos, dos trabalhadores de certa indústria. Suponha que X têm distribuição normal com média de μ anos e desvio padrão de 5 anos.
Uma amostra aleatória, com reposição, de n trabalhadores será selecionada e sejam X1, X2, ... Xn as idades observadas e 
a média desta amostra. Desejando-se que o valor absoluto da diferença entre 
e sua média seja menor do que
6 meses, com probabilidade de 95,4%, o valor de n deverá ser igual a
Atenção: Para responder às questões de números 49 a 53 utilize, dentre as informações dadas a seguir, as que julgar apropriadas.
Se Z tem distribuição normal padrão, então: P(Z < 0,5) = 0,591; P(Z < 1) = 0,841; P(Z < 1,15) = 0,8951; P(Z < 1,17) = 0,879; P(Z < 1,2) = 0,885; P(Z < 1,4) = 0,919; P(Z < 1,64) = 0,95; P(Z < 2) = 0,977; P(Z < 2,06) = 0,98; P(Z < 2,4) = 0,997.
O tempo total para a análise de um processo trabalhista, que chega a um Tribunal Regional do Trabalho, é dado pela soma dos
tempos dos 3 analistas, que o examinam. Sejam Xi , i = 1,2,3, as variáveis aleatórias que representam os tempos, em dias, para
análise dos analistas 1,2 e 3, respectivamente. Sabe-se que o vetor 
em distribuição normal multivariada com vetor de
médias dado por 
e matriz de covariâncias dada por 
onde os valores do vetor μ, são dados em
dias e os da matriz Σ em (dias)². Um processo é selecionado aleatoriamente dentre todos os processos que chegam àquele órgão. A probabilidade do tempo total
para análise se situar entre 42 dias e 45 dias, em %, é igual a
Em um processo de Markov em dois estágios (zero e um) sejam:
Nessas condições
é igual a
A tabela de frequências absolutas abaixo corresponde à distribuição dos valores dos salários dos funcionários de nível médio
lotados em um órgão público no mês de dezembro de 2014.
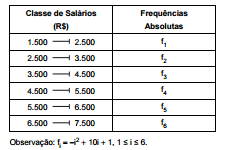
O valor da mediana destes salários, obtido pelo método da interpolação linear, é, em R$, igual a
Em uma empresa, 55% dos empregados são do sexo masculino e a média aritmética dos salários de todos os empregados da
empresa é igual a R$ 3.000,00. Sabe-se que a média aritmética dos salários dos empregados do sexo masculino é igual a média
aritmética dos salários dos empregados do sexo feminino, sendo que os coeficientes de variação são iguais a 10% e 15%,
respectivamente. O desvio padrão dos salários de todos os empregados da empresa é, em R$, de
Os estimadores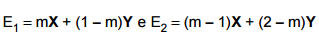 
são utilizados para estimar a média μ de uma população normal
com variância unitária. O parâmetro m é real e (X, Y) corresponde a uma amostra aleatória com reposição da população. Dado
que E2 é mais eficiente que E1 e que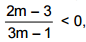 
tem-se que o valor de m que satisfaz estas duas condições é tal que
A variância de uma população normalmente distribuída e de tamanho infinito é desconhecida. Uma amostra aleatória de
tamanho 9 é extraída desta população obtendo-se a média dos elementos da amostra igual a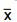 
e o respectivo desvio padrão
amostral igual a 2,7. Considere o objetivo de testar a hipótese H0: μ = 20 (hipótese nula) contra H1: μ ≠ 20 (hipótese alternativa),
ao nível de significância de 5%, com a realização do teste t de Student. Sabe-se que t0,025 corresponde ao quantil da distribuição
t de Student para o teste unicaudal tal que a probabilidade P(t > t0,025) = 0,025, com n graus de liberdade.
A hipótese H0 será rejeitada caso I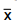 
Atenção: Para responder às questões de números 38 a 40, considere o modelo linear , Yi = α + β + ε sendo i a i-ésima observação, Yi a variável dependente na observação i, X a variável explicativa na observação i e i i ε o erro aleatório com as respectivas hipóteses para a regressão linear simples. Os parâmetros α e β são desconhecidos e suas estimativas (a e b, respectivamente) foram obtidas pelo método dos mínimos quadrados e com base em 20 pares de observações ( X , i Y ), i = 1, 2, ... , 20. Sabe-se que os pontos (10 ; 9,8) e (40 ; 33,8) pertencem à reta de equação Y i = a + bX.
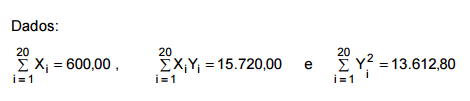
Pelo quadro de análise de variância correspondente, observa-se que
