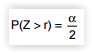Ao vender a peça, o lucro obtido pelo fabricante é de 50 reais se X se distanciar de sua média por, no máximo, 1,5 cm e, é de -10 reais caso contrário. Nessas condições, o lucro esperado por peça do fabricante é, em reais, igual a
Uma variável aleatória X tem distribuição uniforme contínua com média igual a 4 e variância igual a 12. Nessas condições, P(X < 7) é igual a
A função densidade de probabilidade da variável bidimensional contínua (X,Y) é dada por:
Onde K é a constante adequada para tornar f(x,y) uma função densidade de probabilidade.
Nessas condições, P(X < 1/2, Y < 1/2) é igual a
O quadro abaixo apresenta a quantidade de realizações de um determinado evento durante 50 dias.
Se a média aritmética (realizações por dia), ponderada pelo número de dias, é igual à moda da distribuição, então (2m + 3n) é
igual a
A população formada pelos salários dos empregados de um determinado setor é considerada de tamanho infinito, apresentando uma distribuição normal com média μ e desvio padrão populacional igual a R$ 256,00. Uma amostra aleatória de tamanho 225 é extraída desta população obtendo-se um intervalo de confiança de (1 - α) para μ, em R$, igual a [3.271,84 ; 3.328,16]. O valor do escore r da curva normal padrão (Z )tal que a probabilidade
é:
Em três grandes cidades de um estado foram escolhidos aleatoriamente, em cada uma, 100 eleitores. Deseja-se saber, ao nível
de significância α, se o grau de satisfação do desempenho do governador depende da cidade onde os eleitores residem. Em
cada cidade foi perguntado, independentemente, para cada eleitor o que ele achava do desempenho do governador. A tabela
abaixo reproduz o resultado da pesquisa e sabe-se que nenhum eleitor reside em mais de uma cidade.
Utilizou-se o teste qui-quadrado para concluir se eXiste dependência do grau de desempenho com relação às cidades e
verificou-se que o qui-quadrado observado foi inferior ao qui-quadrado tabelado, de acordo com o nível de significância α
estabelecido. Com relação ao teste,
Para testar a eXistência da regressão, a um determinado nível de significância, optou-se pelo teste t de Student, em que foram formuladas as hipóteses H0: β = 0 (hipótese nula) e H1: β ≠ 0 (hipótese alternativa). Sabendo-se que o coeficiente de explicação (R2), definido como sendo o resultado da divisão da variação explicada pela variação total, é igual a 62,5%, tem-se que o valor do t calculado ( tc ) utilizado para comparação com o respectivo t tabelado é tal que
Duas pessoas serão selecionadas ao acaso e com reposição dentre os 1000 eleitores. A probabilidade de exatamente uma ter salário mensal na faixa de salário mínimos 11|----- 17 e preferir o candidato A é, em %, igual a
Um dado não viciado, cujas faces são numeradas de 1 a 6, é lançado e considera-se como sucesso a ocorrência de face superior a 4 . Nessas condições, a probabilidade de serem necessários 5 lançamentos do dado para a obtenção de exatamente 3 sucessos é igual a
Em um determinado órgão público o tempo X, em horas, entre duas solicitações consecutivas, feitas pelo departamento de
recursos humanos, pode ser considerado como tendo distribuição exponencial com média de 5 horas. Nessas condições, a
probabilidade do tempo entre duas solicitações estar compreendido entre 2 horas e 6 horas é, em %, igual a
Dados:
e- 0,2 = 0,819;
e- 0,4 = 0,670;
e- 1,2 = 0,301.
A função de probabilidade conjunta das variáveis X e Y é dada por:
Nessas condições, a esperança condicional de X dado que Y é igual a 2, denotada por E(X|Y = 2) é igual, a
Uma distribuição estatística unimodal, com uma curva de frequência platicúrtica e sendo a média inferior à mediana e a mediana inferior à moda, caracteriza uma distribuição assimétrica à
Seja X uma variável aleatória uniformemente distribuída no intervalo (m , n) em que m e n são desconhecidos. Utiliza-se o método dos momentos para encontrar os estimadores para m e n ( IMAGEM , respectivamente). De uma amostra aleatória da respectiva população de tamanho 8, obteve-se uma média amostral igual a 6 e o momento de segunda ordem igual a 37,6875. Com base nos resultados desta amostra, encontra-se que o resultado da divisão de IMAGEM por IMAGEM apresenta um valor igual a
A amostra aleatória { X1, X2, X3, ... , X9 } foi extraída de uma população normal de tamanho infinito com variância (σ2)
desconhecida.
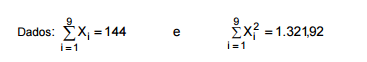
Com base nesta amostra, deseja-se obter um intervalo de confiança de 90% para a média μ da população utilizando a
distribuição t de Student levando em conta a tabela a seguir.

Este intervalo é igual a
Atenção: Para responder às questões de números 37 e 38 considere o modelo de regressão linear simples correspondente à equação Yi = α + βXi + ϵi (i = 1, 2, 3, ...) que é utilizado por uma empresa para prever o seu faturamento bruto (Y), em milhões de reais, em função do dispêndio com material promocional (X), também em milhões de reais. Os parâmetros α e β são desconhecidos, ϵi corresponde ao erro aleatório com as respectivas hipóteses do modelo de regressão linear simples e i refere-se à i-ésima observação das variáveis. As estimativas de α e β (a e b, respectivamente) foram obtidas pelo método dos mínimos quadrados, com base em 10 pares de observações (Xi , Yi ).
Considerando a equação da reta obtida pelo método dos mínimos quadrados, obtém-se que o acréscimo do faturamento bruto, em milhões de reais, cada vez que se decide aumentar em 1 milhão de reais o dispêndio com material promocional é de