Um laboratório farmacêutico
realizou uma pesquisa, perguntando qual o
medicamento utilizado no combate à dor de
cabeça na cidade de Porto Alegre. Para
responder à pesquisa, foram selecionadas,
aleatoriamente, 2.250 pessoas residentes na
cidade de Porto Alegre. Sobre essa pesquisa, é
possível afirmar que foi realizada a partir de
uma
A probabilidade de chover em determinado dia, dado que choveu no dia anterior, é de 0,6 . Se a probabilidade de chover em um dia qualquer é de 0,3, a probabilidade de dois dias de chuva seguidos é de:
A função distribuição de probabilidade acumulada da variável
“número de anos de experiência de magistrados" de um dado
tribunal é dada por:

Então, a probabilidade de que um magistrado escolhido ao acaso
tenha experiência maior do que cinco anos e menor ou igual a 15
anos é igual a:
Suponha que X e Y são variáveis aleatórias independentes, definidas no mesmo intervalo, com funções de densidade fx (x ) e fy(y ), respectivamente. Então a função de densidade conjunta, naquele intervalo, é dada por:
Suponha que o valor das causas de ações (X ) do juizado especial
de certa localidade seja normalmente distribuído com média 20
(salários mínimos) e variância 25 . Além disso, estão disponíveis as
seguintes informações da normal-padrão (Z ):
P(|Z|>1,25)=0,21, P(|Z|>1,50)=0,13, P(|Z|>1,75)=0,08
Então a probabilidade de que P(X > 26,25) é de:
Seja X1, X2, X3, ... ..., X25, um conjunto de variáveis aleatórias que
representa o número de processos autuados por dia nas 25 varas
que compõem um tribunal, todas identicamente distribuídas com
média 15 e variância 16. Adicionalmente, são dadas as seguintes
informações sobre a normal-padrão:
P(|Z|>1,25)=0,21, P(|Z|>1,50)=0,13, P(|Z|>1,75)=0,08
Assim sendo, a probabilidade de que mais de 405 processos
sejam autuados em determinado dia é igual a:
Um levantamento censitário de processos criminais indicou que a
pena média, para determinado tipo de crime, é de 60 meses.
Visando testar a maior severidade dos juízes de certa região foi
extraída uma AAS de tamanho n = 36, constatando-se que a pena
média é de 78 meses. Sabendo que a variância das penas é dada
igual a 3.600 e considerando as informações a seguir da normalpadrão
Z
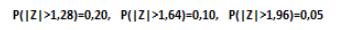
É correto afirmar que:
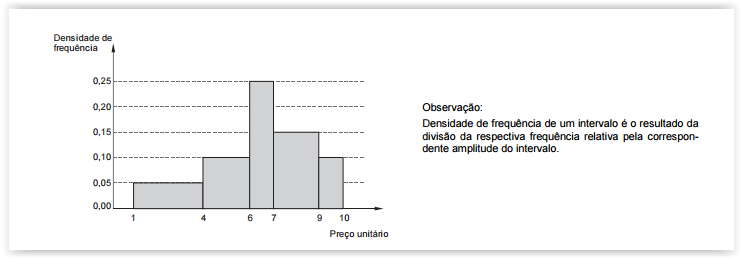
O histograma abaixo representa a distribuição dos preços unitários de custo, em R$, de determinado equipamento de
informática no mercado. No eixo das abscissas constam os intervalos de classe, em R$, e no eixo das ordenadas as respectivas
densidades de frequências em (R$)-1
Considerando os intervalos de classe fechados à esquerda e abertos à direita, se 105 preços apresentam valores menores que
R$ 6,00, então o número de preços que apresentam valores iguais ou superiores a R$ 4,00 é
Sabendo-se que de uma população, com função densidade f(x )= αe-αx (x ≥ 0), extraiu-se uma amostra de tamanho 8 verificando-se com base nesta amostra, que pelo método dos momentos, a estimativa de α foi igual a 0,04. A soma dos valores de todos os elementos desta amostra apresentou um valor igual a
Considere uma população e uma amostra aleatória respectiva de tamanho n representando toda esta população. A metodologia bootstrap é um tipo de reamostragem consistindo em gerar novas amostras
Considerando a equação da reta obtida pelo método dos mínimos quadrados, tem-se que o valor para X tal que Y = 15 é
Uma pessoa será selecionada ao acaso deste grupo de 1000 eleitores. A probabilidade de ela ter salário mensal inferior a 11 salários mínimos ou votar no candidato B é, em %, igual a
Suponha que X e Y sejam variáveis aleatórias independentes com distribuição geométrica com médias dadas, respectivamente,
por 3 e 4. Considere que X e Y representam o número de repetições do experimento até a ocorrência do primeiro sucesso.
Nessas condições, a probabilidade denotada por P(X ≤ 2,Y = 3) é igual a
Seja (X1, X2, ... Xn) uma amostra aleatória simples da variável aleatória X que representa os pesos de crianças recém-nascidas
do sexo feminino em determinada população. Sabe-se que:
Nessas condições, o valor de n para que a diferença, em valor absoluto, entre X e μ seja, no máximo, 0,2 kg, com probabilidade
de 92,8%, é igual a
A função de distribuição acumulada da variável aleatória X é dada por:
Nessas condições, a variância de X é igual a