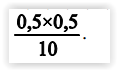Considere um processo de amostragem de uma população finita
cuja variável de interesse seja binária e assuma valor 0 ou 1, sendo
a proporção de indivíduos com valor 1 igual a p = 0,3. Considere,
ainda, que a probabilidade de cada indivíduo ser sorteado seja
a mesma para todos os indivíduos da amostragem e que, após cada
sorteio, haja reposição do indivíduo selecionado na amostragem.
A partir dessas informações, julgue os itens subsequentes.
Se, em uma amostra de tamanho n = 10, os valores observados
forem A = {1, 0, 1, 0, 1, 0, 0, 1, 0, 0}, o erro padrão da média
amostral será igual a
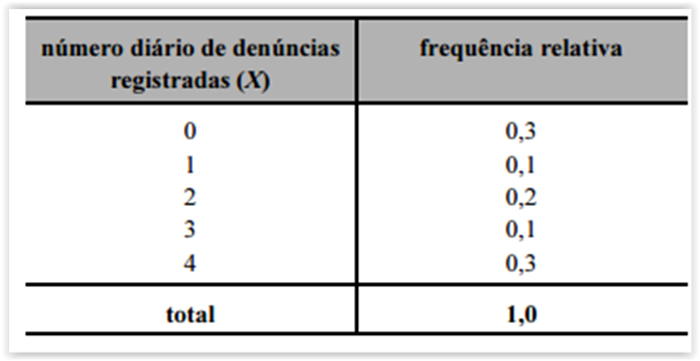
A variável X é do tipo qualitativo nominal.
Considere que Y seja uma variável aleatória geométrica que representa o número de erros cometidos por um atendente no preenchimento de formulários e que a função de probabilidade de Y seja definida por P(Y = k) = 0,9 × (0,1) k , em que k = 0, 1, 2, ... . A partir dessas informações, julgue os itens que se seguem.
A variável Y segue uma distribuição com assimetria negativa.
Considerando que Z e W sejam variáveis aleatórias independentes que seguem distribuição normal padrão, julgue os itens subsequentes.
A soma dos quadrados Z² + W² segue distribuição t de Student.
Considerando que uma amostra aleatória simples X 1, X2, ..., Xn tenha sido retirada de uma população exponencial com média igual a 5, julgue os próximos itens, relativos à média amostral
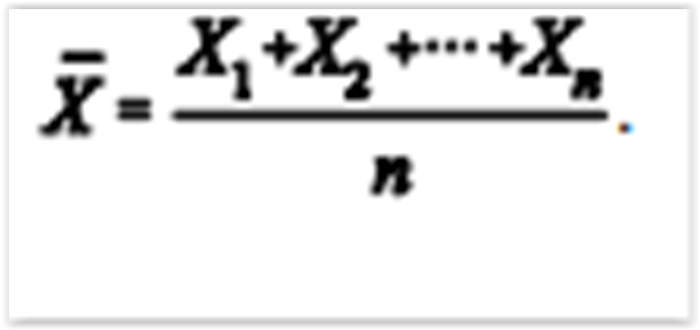
Para um valor n suficientemente grande,

Considerando que uma amostra aleatória simples X 1, X2, ..., Xn tenha sido retirada de uma população exponencial com média igual a 5, julgue os próximos itens, relativos à média amostral
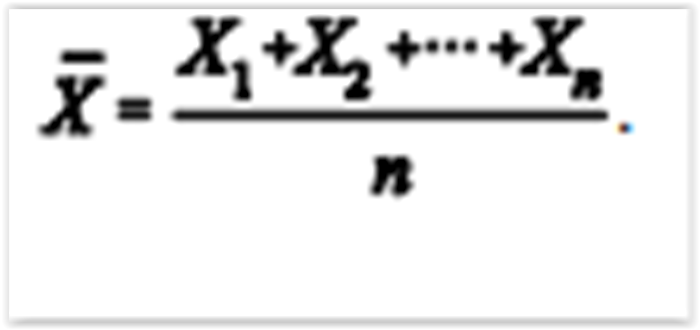
Se n = 10, a distribuição amostral de
Suponha que o tribunal de contas de determinado estado disponha de 30 dias para analisar as contas de 800 contratos firmados pela administração. Considerando que essa análise é necessária para que a administração pública possa programar o orçamento do próximo ano e que o resultado da análise deve ser a aprovação ou rejeição das contas, julgue os itens a seguir. Sempre que necessário, utilize que P(Z > 1,96) = 0,025 e P(Z > 1,645) = 0,05, em que Z representa a variável normal padronizada.
Em uma amostra aleatória simples de 400 elementos, o peso amostral de cada elemento será maior ou igual a 2.
A respeito de uma amostra de tamanho n = 10, com os valores amostrados {0,10, 0,06, 0,10, 0,12, 0,08, 0,10, 0,05, 0,15, 0,14, 0,11}, extraídos de determinada população, julgue os itens seguintes.
Dado que a variância populacional é desconhecida e os dados seguem uma distribuição normal, é correto afirmar que o teste t para a média populacional possui 10 graus de liberdade.
A respeito de uma amostra de tamanho n = 10, com os valores amostrados {0,10, 0,06, 0,10, 0,12, 0,08, 0,10, 0,05, 0,15, 0,14, 0,11}, extraídos de determinada população, julgue os itens seguintes.
A estimativa pontual da média a partir dessa amostra é inferior a 0,09
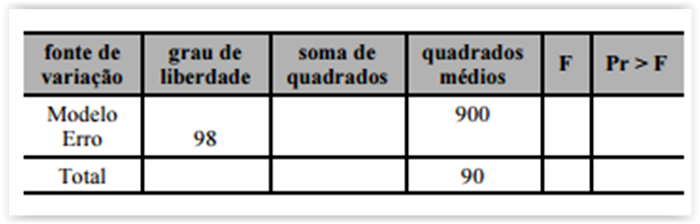
Considerando um modelo de regressão linear simples, para
averiguar se existe alguma relação entre o salário pago — Y — para
uma pessoa em cargo comissionado e o tempo de trabalho — X —
dessa pessoa na campanha de determinado padrinho político eleito,
foi escolhida uma amostra de indivíduos em cargos comissionados
cujos resultados estão apresentados nessa tabela.
Com base nessa situação hipotética e nos dados apresentados na
tabela, julgue os itens que se seguem, relativos à análise de
regressão e amostragem.
A amostra é composta por 100 pessoas em cargos comissionados.
Em estudo acerca da situação do CNPJ das empresas de determinado município, as empresas que estavam com o CNPJ regular foram representadas por 1, ao passo que as com CNPJ irregular foram representadas por 0. Considerando que a amostra {0, 1, 1, 0, 0, 1, 0, 1, 0, 1, 1, 0, 0, 1, 1, 0, 1, 1, 1, 1} foi extraída para realizar um teste de hipóteses, julgue os itens subsequentes.
A estatística do teste para testar a hipótese H0: P = 0,5 contra
H1: P ≠ 0,5, em que P representa a proporção de empresas cujo
CNPJ está regular, é maior que 2.
Responda às questões 50, 51 e 52, com base no texto abaixo. Considere duas urnas contendo as mesmas quantidades de bolas, com a mesma proporção de cores, 3 bolas grenás e 2 verdes. Transfere-se aleatoriamente uma bola de uma urna para a outra. Em seguida, sortea-se uma bola da urna que passou a ter uma bola a mais.
A probabilidade de ter saído a bola grená na primeira extração,
sabendo-se que saiu bola verde na segunda extração é de:
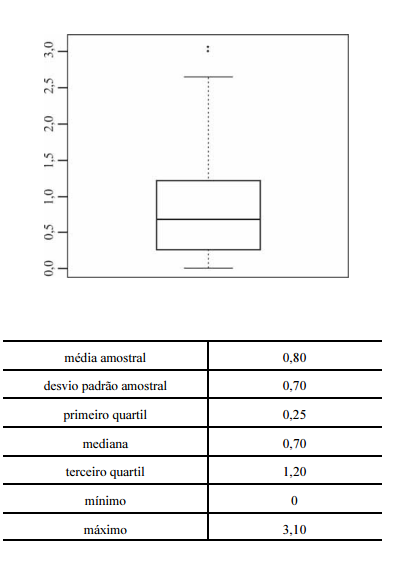
Um indicador de desempenho X permite avaliar
a qualidade dos processos de governança de instituições públicas.
A figura mostra, esquematicamente, a sua distribuição, obtida
mediante estudo amostral feito por determinada agência de
pesquisa. A tabela apresenta estatísticas descritivas referentes a essa
distribuição.
Com base nessas informações, julgue os itens a seguir.
A distribuição do indicador X apresenta assimetria positiva (ou à direita).
Se o tempo de espera por atendimento (T, em minutos) em
determinada repartição pública segue uma distribuição exponencial
com média igual a 30 minutos, então
o desvio padrão da variável aleatória T é igual a 30 minutos.
Se as variáveis aleatórias X e Y seguem distribuições de Bernoulli,
tais que P[X = 1] = P[Y = 0] = 0,9, então
a distribuição de X 2 é Bernoulli com média igual a 0,81