Sabe-se que as notas de uma prova têm distribuição Normal
com média μ = 6,5 e variância α = 4²
. Adicionalmente, são
conhecidos alguns valores tabulados da normal-padrão.
Onde,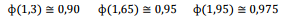
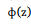é a função distribuição acumulada da Normal Padrão.
Considerando-se que apenas os 10% que atinjam as maiores notas
serão aprovados, a nota mínima para aprovação é:
Sabe-se que as notas de uma prova têm distribuição Normal
com média μ = 6,5 e variância α = 4²
. Adicionalmente, são
conhecidos alguns valores tabulados da normal-padrão.
Onde,
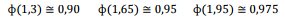
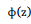é a função distribuição acumulada da Normal Padrão.
Considerando-se que apenas os 10% que atinjam as maiores notas
serão aprovados, a nota mínima para aprovação é:
Um auditor foi convocado para verificar se o valor de Y, doado para a campanha de determinado candidato, estava relacionado ao valor de X, referente a contratos firmados após a sua eleição.
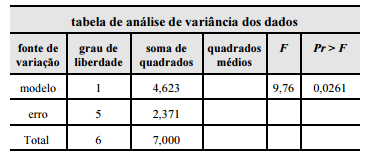
Com base na situação hipotética e na tabela apresentadas, julgue os itens que se seguem, considerando-se que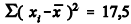 
e 
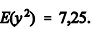
A média de Y (valor doado para a campanha) é maior que 2.
Tendo como referência o gráfico precedente, que mostra os valores,
em bilhões de reais, relativos à arrecadação de receitas e aos gastos
com despesas do estado do Paraná nos doze meses do ano de 2015,
assinale a opção correta.
Se X for uma variável aleatória normal com média 0,8 e variância 0,4, e P(X ≤ x) representar a função de distribuição de probabilidade acumulada dessa variável X, para x ∈ R, então
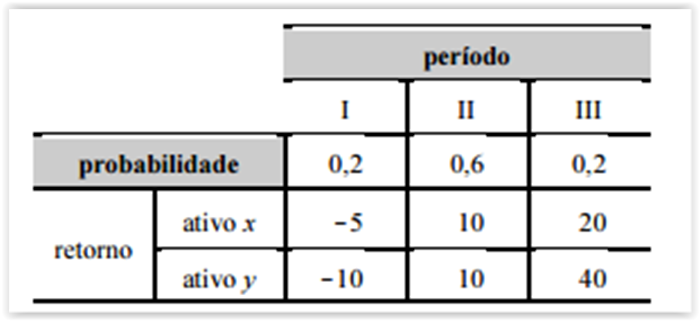
A tabela precedente mostra os ativos x e y (variáveis aleatórias) e seus retornos. Considerando que as variâncias de x e y sejam
respectivamente, julgue os próximos σx 2 σy 2 itens.
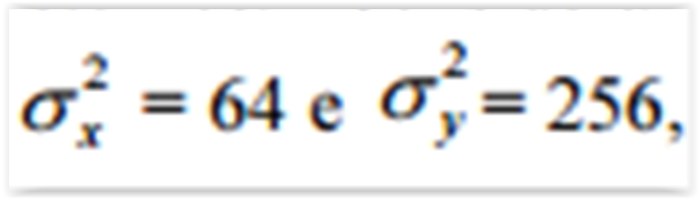
A covariância entre x e y é igual a 122.
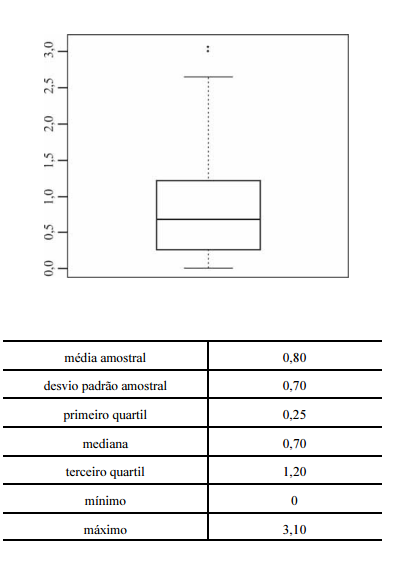
Um indicador de desempenho X permite avaliar
a qualidade dos processos de governança de instituições públicas.
A figura mostra, esquematicamente, a sua distribuição, obtida
mediante estudo amostral feito por determinada agência de
pesquisa. A tabela apresenta estatísticas descritivas referentes a essa
distribuição.
Com base nessas informações, julgue os itens a seguir.
O coeficiente de variação da distribuição de X é inferior a 0,8.
Se o tempo de espera por atendimento (T, em minutos) em
determinada repartição pública segue uma distribuição exponencial
com média igual a 30 minutos, então
a probabilidade de ocorrer o evento [T = 30], isto é, P([T=30]), é igual a zero.
Se as variáveis aleatórias X e Y seguem distribuições de Bernoulli,
tais que P[X = 1] = P[Y = 0] = 0,9, então
as variâncias de X e Y são iguais.
Uma amostra aleatória simples X1, X2, ..., Xn foi retirada de uma
população normal com média e desvio padrão iguais a 10. Julgue
os próximos itens, a respeito da média amostral = [X1 + X2 + ... + Xn]/n.
A estatística segue uma distribuição quiquadrado com 1 grau de liberdade.
A respeito de uma variável aleatória contínua U, uniformemente
distribuída no intervalo [0, 1], julgue os seguintes itens.
P(U > 1/10) = 0,9
Uma amostra aleatória, com n = 16 observações
independentes e identicamente distribuídas (IID), foi obtida a partir
de uma população infinita, com média e desvio padrão
desconhecidos e distribuição normal.
Tendo essa informação como referência inicial, julgue os seguintes
itens.
A potência de um teste de hipóteses corresponde à probabilidade de se rejeitar a hipótese nula, dado que a hipótese nula é correta.
Uma amostra aleatória, com n = 16 observações
independentes e identicamente distribuídas (IID), foi obtida a partir
de uma população infinita, com média e desvio padrão
desconhecidos e distribuição normal.
Tendo essa informação como referência inicial, julgue os seguintes
itens.
Se a variância amostral for igual a 4,0, o erro padrão da média amostral será igual a 0,5
Uma regressão linear simples é expressa por Y = a + b × X + e,
em que o termo e corresponde ao erro aleatório da regressão e os
parâmetros a e b são desconhecidos e devem ser estimados a partir
de uma amostra disponível. Assumindo que a variável X é não
correlacionada com o erro e, julgue os itens subsecutivos, nos quais
os resíduos das amostras consideradas são IID, com distribuição
normal, média zero e variância constante.
Para uma amostra de tamanho n = 25, em que a covariância amostral para o par de variáveis X e Y seja Cov(X, Y) = 20,0, a variância amostral para a variável Y seja Var(Y ) = 4,0 e a variância amostral para a variável X seja Var(X ) = 5,0, a estimativa via estimador de mínimos quadrados ordinários para o coeficiente b é igual a 5,0.
Uma regressão linear simples é expressa por Y = a + b × X + e,
em que o termo e corresponde ao erro aleatório da regressão e os
parâmetros a e b são desconhecidos e devem ser estimados a partir
de uma amostra disponível. Assumindo que a variável X é não
correlacionada com o erro e, julgue os itens subsecutivos, nos quais
os resíduos das amostras consideradas são IID, com distribuição
normal, média zero e variância constante.
A variável Y é denominada variável explicativa, e a variável X é denominada variável dependente.
