Uma amostra aleatória simples X1, X2, ..., Xn foi retirada de uma
população normal com média e desvio padrão iguais a 10. Julgue
os próximos itens, a respeito da média amostral = [X1 + X2 + ... + Xn]/n.
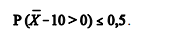
A respeito de uma variável aleatória contínua U, uniformemente
distribuída no intervalo [0, 1], julgue os seguintes itens.
Se U1, U2, ..., Un é uma amostra aleatória simples retirada da distribuição U, então, para n suficientemente grande, a soma U1 + U2 + ... + Un segue aproximadamente uma distribuição normal.
Uma amostra aleatória, com n = 16 observações
independentes e identicamente distribuídas (IID), foi obtida a partir
de uma população infinita, com média e desvio padrão
desconhecidos e distribuição normal.
Tendo essa informação como referência inicial, julgue os seguintes
itens.
Em um intervalo de 95% de confiança para a média populacional em questão, caso se aumente o tamanho da amostra em 100 vezes (passando a 1.600 observações), a largura total do intervalo de confiança será reduzida à metade.
Uma amostra aleatória, com n = 16 observações
independentes e identicamente distribuídas (IID), foi obtida a partir
de uma população infinita, com média e desvio padrão
desconhecidos e distribuição normal.
Tendo essa informação como referência inicial, julgue os seguintes
itens.
Se a média amostral for igual a 3,2 e a variância amostral, igual a 4,0, o estimador de máxima verossimilhança para a média populacional será igual a 1,6
Considerando uma população finita em que a média da variável de
interesse seja desconhecida, julgue os itens a seguir.
Se os totais de observações na amostra dos processos de amostragem aleatória simples e de amostragem aleatória estratificada forem iguais, o desvio padrão do estimador da média por amostragem aleatória simples será menor que o por amostragem estratificada.
Uma regressão linear simples é expressa por Y = a + b × X + e,
em que o termo e corresponde ao erro aleatório da regressão e os
parâmetros a e b são desconhecidos e devem ser estimados a partir
de uma amostra disponível. Assumindo que a variável X é não
correlacionada com o erro e, julgue os itens subsecutivos, nos quais
os resíduos das amostras consideradas são IID, com distribuição
normal, média zero e variância constante.
Se, depois de realizado um teste de hipóteses com hipótese nula H0: b = 0 para o coeficiente b, for encontrado um p-valor menor que 0,000001, não existirá uma relação linear estatisticamente significante entre as variáveis X e Y.
Considere um processo de amostragem de uma população finita
cuja variável de interesse seja binária e assuma valor 0 ou 1, sendo
a proporção de indivíduos com valor 1 igual a p = 0,3. Considere,
ainda, que a probabilidade de cada indivíduo ser sorteado seja
a mesma para todos os indivíduos da amostragem e que, após cada
sorteio, haja reposição do indivíduo selecionado na amostragem.
A partir dessas informações, julgue os itens subsequentes.
Caso, em uma amostra de tamanho n = 10, os valores observados sejam A = {1, 0, 1, 0, 1, 0, 0, 1, 0, 0}, a estimativa via estimador de máxima verossimilhança para a média populacional será igual a 0,4
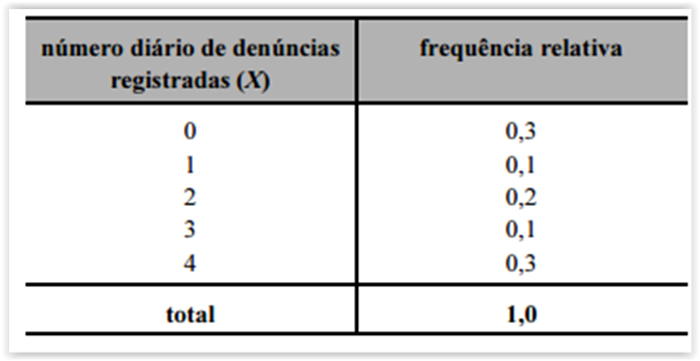
A amplitude total da amostra é igual ou superior a 5.
A mediana do número diário de denúncias registradas é igual a 2.
Considerando que Z e W sejam variáveis aleatórias independentes que seguem distribuição normal padrão, julgue os itens subsequentes.
A transformação 6Z + 3 resulta em uma distribuição normal com variância igual a 9.
Considerando que Z e W sejam variáveis aleatórias independentes que seguem distribuição normal padrão, julgue os itens subsequentes.
Var(2Z + 3W) < 10.
O número de acidentes de trabalho em determinada obra pública
no mês k segue uma distribuição de Poisson Wk com média
igual a 1 acidente por mês. Considerando uma amostra aleatória
simples W1, W2,..., Wn, julgue o item a seguir, acerca da soma
Sn = W1 % W2 % ...% Wn.
O total de acidentes Sn segue distribuição de Poisson com média igual a n.
Suponha que o tribunal de contas de determinado estado disponha de 30 dias para analisar as contas de 800 contratos firmados pela administração. Considerando que essa análise é necessária para que a administração pública possa programar o orçamento do próximo ano e que o resultado da análise deve ser a aprovação ou rejeição das contas, julgue os itens a seguir. Sempre que necessário, utilize que P(Z > 1,96) = 0,025 e P(Z > 1,645) = 0,05, em que Z representa a variável normal padronizada.
Considerando-se que, no ano anterior ao da análise em questão,
80% dos contratos tenham sido aprovados e que 0,615 seja
o valor aproximado de 1,962
× 0,8 × 0,2, é correto afirmar que
a quantidade de contratos de uma amostra com nível de 95%
de confiança para a média populacional e erro amostral de 5%
é inferior a 160.
Suponha que o tribunal de contas de determinado estado disponha de 30 dias para analisar as contas de 800 contratos firmados pela administração. Considerando que essa análise é necessária para que a administração pública possa programar o orçamento do próximo ano e que o resultado da análise deve ser a aprovação ou rejeição das contas, julgue os itens a seguir. Sempre que necessário, utilize que P(Z > 1,96) = 0,025 e P(Z > 1,645) = 0,05, em que Z representa a variável normal padronizada.
Caso se opte por uma amostra aleatória estratificada, a variância da média amostral será menor ou igual à que seria obtida por amostragem aleatória simples.
A respeito de uma amostra de tamanho n = 10, com os valores amostrados {0,10, 0,06, 0,10, 0,12, 0,08, 0,10, 0,05, 0,15, 0,14, 0,11}, extraídos de determinada população, julgue os itens seguintes.
Para um teste Z ou t de Student bilateral (com pelo menos 9 graus de liberdade), uma estatística do teste menor que 1,5 é considerada não significativa para o nível de significância de 5%.