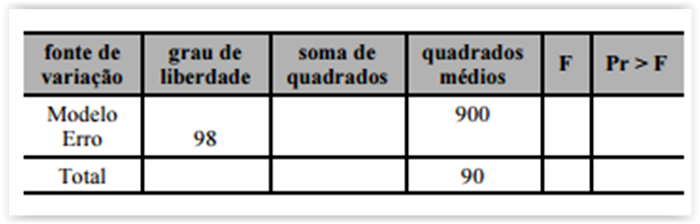
Considerando um modelo de regressão linear simples, para
averiguar se existe alguma relação entre o salário pago — Y — para
uma pessoa em cargo comissionado e o tempo de trabalho — X —
dessa pessoa na campanha de determinado padrinho político eleito,
foi escolhida uma amostra de indivíduos em cargos comissionados
cujos resultados estão apresentados nessa tabela.
Com base nessa situação hipotética e nos dados apresentados na
tabela, julgue os itens que se seguem, relativos à análise de
regressão e amostragem.
O modelo possui ajuste superior a 15%.
Em estudo acerca da situação do CNPJ das empresas de determinado município, as empresas que estavam com o CNPJ regular foram representadas por 1, ao passo que as com CNPJ irregular foram representadas por 0. Considerando que a amostra {0, 1, 1, 0, 0, 1, 0, 1, 0, 1, 1, 0, 0, 1, 1, 0, 1, 1, 1, 1} foi extraída para realizar um teste de hipóteses, julgue os itens subsequentes.
Uma vez que a amostra é menor que 30, a estatística do teste
utilizada segue uma distribuição t de Student.
100 A estatística do teste para testar a hipótese H0: P = 0,5 contra
H1: P … 0,5, em que P representa a proporção de empresas cujo
CNPJ está regular, é maior que 2.
Na tabela a seguir, estão listados os possíveis retornos
de um projeto de investimentos e as respectivas
probabilidades de ocorrências desses retornos:
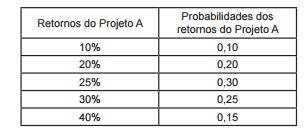
O retorno médio esperado do Projeto A é igual a
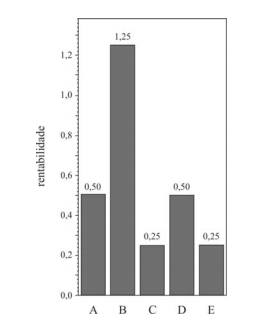
A rentabilidade média dos fundos de investimento é maior
que 0,7.
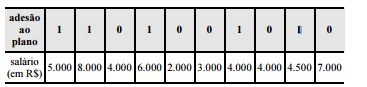
Considerando que os dados na tabela mostram salários de diferentes servidores que aderiram (1) ou não aderiram (0) a determinado plano de previdência complementar, julgue os itens subsecutivos.
A média dos salários do grupo que aderiu ao plano de
previdência complementar é menor que a do que não aderiu
ao plano.
Se satisfação no trabalho e saúde no trabalho forem indicadores com variâncias populacionais iguais a 8 e 2, respectivamente, e se a covariância populacional entre esses indicadores for igual a 3, então a correlação populacional entre satisfação no trabalho e saúde no trabalho será igual a
Após a extração de uma amostra, as observações obtidas são
tabuladas, gerando a seguinte distribuição de frequências:
Considerando que E(X ) = Média de X, Mo(X ) = Moda de X e Me(X )
= Mediana de X, é correto afirmar que:
Sejam Y, X, Z e W variáveis aleatórias tais que Z = 2.Y - 3.X,
sendo E( X²) = 25, E( X) = 4, Var( Y)=16, Cov(X,Y) = 6 .
Então a variância de Z é:
Após a extração de uma amostra, as observações obtidas são
tabuladas, gerando a seguinte distribuição de frequências:
Considerando que E(X ) = Média de X, Mo(X ) = Moda de X e Me(X )
= Mediana de X, é correto afirmar que:
Após a extração de uma amostra, as observações obtidas são
tabuladas, gerando a seguinte distribuição de frequências:
Considerando que E(X ) = Média de X, Mo(X ) = Moda de X e Me(X )
= Mediana de X, é correto afirmar que:
As notas em uma prova de matemática dos alunos de uma determinada escola estão resumidas no seguinte gráfico Boxplot. Analise-o.
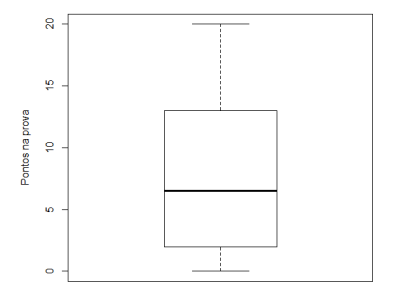
Sabendo que a prova valia 20 pontos, pode-se afirmar que
Um prefeito acredita que os habitantes de seu município estão lendo pouco, pois a biblioteca municipal está sempre
com pouco movimento. Para mudar essa situação, ele pensou em fazer uma campanha para estimular a leitura,
entretanto precisa comprovar estatisticamente que a média de livros lidos por habitante do município está abaixo da
média nacional para conseguir a liberação da verba para executar a campanha.
Informações adicionais
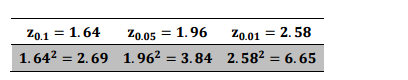
Qual o tamanho da amostra que o prefeito precisa coletar usando amostragem aleatória simples se ele deseja ter
90% de confiança e margem de erro 1, sabendo através de um estudo prévio que σ2
Com respeito à Inferência Bayesiana, analise as afirmativas a seguir.
I. O ideal quando se tem pouca informação inicial sobre um parâmetro θ é utilizar uma distribuição a priori p(θ) muito
informativa.
II. A distribuição a priori traz de maneira resumida a informação contida nos dados amostrais.
III. A distribuição a priori sempre influencia mais na distribuição a posteriori que os dados amostrais.
Está(ão) INCORRETA(S ) a(s) afirmativa(s)
Sabe-se que as notas de uma prova têm distribuição Normal
com média μ = 6,5 e variância α = 4²
. Adicionalmente, são
conhecidos alguns valores tabulados da normal-padrão.
Onde,
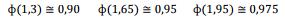
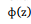é a função distribuição acumulada da Normal Padrão.
Considerando-se que apenas os 10% que atinjam as maiores notas
serão aprovados, a nota mínima para aprovação é:
Após a extração de uma amostra, as observações obtidas são
tabuladas, gerando a seguinte distribuição de frequências:
Considerando que E(X ) = Média de X, Mo(X ) = Moda de X e Me(X )
= Mediana de X, é correto afirmar que:
