Sejam Y, X, Z e W variáveis aleatórias tais que Z = 2.Y - 3.X,
sendo E(X²) = 25, E( X) = 4, Var(Y) =16, Cov(X,Y ) =2.
Então a variância de Z é:
Sejam Y, X, Z e W variáveis aleatórias tais que Z = 2.Y - 3.X,
sendo E(X²) = 25, E( X) = 4, Var (X ) = 16, Cov( X,Y) =6.
Então a variância de Z é:
Após a extração de uma amostra, as observações obtidas são
tabuladas, gerando a seguinte distribuição de frequências:

Considerando que E(X ) = Média de X, Mo(X ) = Moda de X e Me(X )
= Mediana de X, é correto afirmar que:
Após a extração de uma amostra, as observações obtidas são
tabuladas, gerando a seguinte distribuição de frequências:

Considerando que E(X ) = Média de X, Mo(X ) = Moda de X e Me(X )
= Mediana de X, é correto afirmar que:
Sejam Y, X, Z e W variáveis aleatórias tais que Z = 2.Y - 3.X,
sendo E(X² ) = 25, E(X) = 4, V (Y) = 16, Cov(x,y) =6 .
Então a variância de Z é:
Considerando-se que apenas os 10% que atinjam as maiores notas serão aprovados, a nota mínima para aprovação é:
Após a extração de uma amostra, as observações obtidas são
tabuladas, gerando a seguinte distribuição de frequências:

Considerando que E(X ) = Média de X, Mo(X ) = Moda de X e Me(X )
= Mediana de X, é correto afirmar que:
Certo exame de sangue é capaz de detectar uma doença em 95% dos pacientes que estão doentes de fato. Além disso, ele detecta, erroneamente, a doença em 3% das pessoas saudáveis que fazem o exame (“falso positivo”). Sabendo que a doença atinge 5% da população, qual a probabilidade de uma pessoa estar doente dado que o exame detectou a doença?
O SAC de uma empresa recebe uma ligação a cada 20s. Qual a probabilidade de que em um minuto ele receba
exatamente duas ligações, sabendo que as ligações ocorrem de maneira independente uma das outras?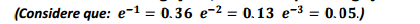
Sobre as técnicas de amostragem, assinale a afirmativa correta.
Calcule o valor de c para que f(x,y) seja uma função de densidade de probabilidade conjunta de X e Y.
Depois calcule a função de densidade de probabilidade condicional de X dado Y = y, em que 0 < y < 2 . Assinale a
alternativa que apresenta o valor de c e a função de densidade de probabilidade condicional pedida.
Após a extração de uma amostra, as observações obtidas são
tabuladas, gerando a seguinte distribuição de frequências:

Considerando que E(X ) = Média de X, Mo(X ) = Moda de X e Me(X )
= Mediana de X, é correto afirmar que:
Após a extração de uma amostra, as observações obtidas são
tabuladas, gerando a seguinte distribuição de frequências:

Considerando que E(X ) = Média de X, Mo(X ) = Moda de X e Me(X )
= Mediana de X, é correto afirmar que:
Sejam Y, X, Z e W variáveis aleatórias tais que Z = 2.Y - 3.X,
sendo E(X²) = 25, E(X ) = 4, Var (Y) = 16, Cov(X,Y ) .
Então a variância de Z é:
Sabe-se que as notas de uma prova têm distribuição Normal
com média μ = 6,5 e variância α = 4²
. Adicionalmente, são
conhecidos alguns valores tabulados da normal-padrão.
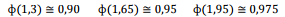
Onde, 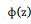 é a função distribuição acumulada da Normal Padrão.
é a função distribuição acumulada da Normal Padrão.
Considerando-se que apenas os 10% que atinjam as maiores notas
serão aprovados, a nota mínima para aprovação é:


