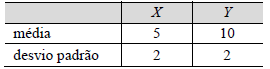
Com base nas informações apresentadas na tabela precedente e considerando que a covariância entre as variáveis X e Y seja igual a 3, julgue o item que se segue
O coeficiente de determinação (ou de explicação) da reta de regressão linear da variável X em função da variável Y é igual ou superior a 0,60.
Considerando que o conjunto de dados apresentado represente uma realização de uma amostra aleatória simples de tamanho n = 5 retirada de uma população X, cuja função de probabilidade acumulada é escrita como
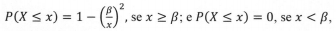
em que ß é o parâmetro desconhecido, julgue o item que se segue
A média amostral é uma estatística suficiente para a estimação do parâmetro ß.
Considere que X e Y sejam variáveis aleatórias contínuas que se distribuem conjuntamente conforme a função de densidade
f (x, y) = x + y, na qual O <x< 1 e O <y< 1.
Com base nessas informações, julgue o item seguinte
Por estudos estatísticos, estima-se que um cliente de um certo banco tem 75% de probabilidade de ir para atendimento de caixa eletrônico, e 25% de ir para um atendimento personalizado.
Em uma amostra de quatro clientes entrando no banco, qual é a probabilidade de que a maioria deles se dirija ao atendimento personalizado?
Com base em uma amostra aleatória simples de tamanho n = 16 retirada de uma população normal com média desconhecida μ e variância a2= 9, deseja-se testar a hipótese nula H1: μ = 0 contra a hipótese alternativa H0: μ ≠ 0 por meio da estatística 
, na qual 
denota a média amostral.
Com respeito a esse teste de hipóteses, julgue o item a seguir, sabendo que o valor da média amostral observado na amostra foi igual a 1 e que, relativo a esse teste, o P-valor foi igual a 0,18.
Sob a hipótese nula, a estatística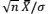 
segue uma distribuição t de Student com 15 graus de liberdade.
Com base em uma amostra aleatória simples de tamanho n = 16 retirada de uma população normal com média desconhecida μ e variância a2= 9, deseja-se testar a hipótese nula H1: μ = 0 contra a hipótese alternativa H0: μ ≠ 0 por meio da estatística , na qual denota a média amostral.
Com respeito a esse teste de hipóteses, julgue o item a seguir, sabendo que o valor da média amostral observado na amostra foi igual a 1 e que, relativo a esse teste, o P-valor foi igual a 0,18.
O P-valor é uma medida que representa a potência do teste em tela.
Suponha que o número diário (X) de transações bancárias registradas em determinada conta bancária se distribua conforme uma distribuição de Poisson. Com respeito ao total semanal de transações bancárias registradas nessa conta bancária, denotada como Y= X1 + X2 + X3 + X4 + X5 em que {X1,… , X5} representa uma amostra aleatória simples retirada de uma distribuição de Poisson com média igual a 5 transações por dia, julgue o seguinte item
Se µ e σ representam, respectivamente, a média e o desvio padrão da variável aleatória Y, então o Teorema Central do Limite estabelece que a quantidade segue a distribuição normal padrão.
Um remédio para baixar a pressão arterial foi testado em pessoas com hipertensão. O referido medicamento foi comparado a outro medicamento que já estava em uso no mercado, por meio de amostragens aleatórias simples. Um teste t foi implementado para verificar se a pressão arterial dos testados baixava mais, em média, com o uso do novo remédio. Os pesquisadores escolheram um nível de significância de 0,01. Se o remédio baixasse a pressão arterial em mais que certa quantidade, p, o fabricante mudaria sua linha de produção para produzir o novo remédio. A potência do teste para detectar uma redução dessa quantidade, p, foi 0,9.
Com relação a essa situação hipotética, julgue o item que se segue.
Se o verdadeiro valor da redução média de pressão do novo remédio fosse igual a p, então existiria uma chance de 90% de o teste ter detectado essa diferença
Um remédio para baixar a pressão arterial foi testado em pessoas com hipertensão. O referido medicamento foi comparado a outro medicamento que já estava em uso no mercado, por meio de amostragens aleatórias simples. Um teste t foi implementado para verificar se a pressão arterial dos testados baixava mais, em média, com o uso do novo remédio. Os pesquisadores escolheram um nível de significância de 0,01. Se o remédio baixasse a pressão arterial em mais que certa quantidade, p, o fabricante mudaria sua linha de produção para produzir o novo remédio. A potência do teste para detectar uma redução dessa quantidade, p, foi 0,9.
Com relação a essa situação hipotética, julgue o item que se segue.
Se fosse aumentado o tamanho da amostra, seria possível diminuir o nível de significância e aumentar a potência do teste
Uma central de assistência técnica de celulares trabalha com três modelos de um mesmo fabricante. Para melhor organizar seu sistema, foi medido o tempo de serviço para o conserto de cada aparelho, desde a chegada do pedido de manutenção até a entrega do aparelho consertado, e cada um desses prazos foi classificado como Curto, Médio ou Longo.
A Tabela abaixo mostra a distribuição dos tempos de serviço para cada um dos três modelos aos quais a empresa prestou assistência em 2020.
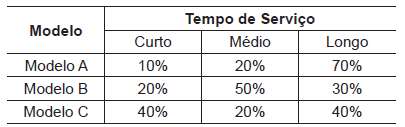
Considerando-se que, ao longo do ano de 2020, essa empresa reparou 1.000 unidades do modelo A, 600 unidades do modelo B e 400 unidades do modelo C, qual foi a porcentagem destes atendimentos, nesse período, que tiveram tempo de serviço Curto ou Médio?
A respeito do conjunto de dados {11, 6, 28, 51, 49, 32, 33}, julgue o item a seguir.
Esse conjunto de dados possui variância amostral inferior a 300.
Um estudo objetivou avaliar a evolução do número mensal Y de milhares de ocorrências de certo tipo de crime em determinado ano. Com base no método dos mínimos quadrados ordinários, esse estudo apresentou um modelo de regressão linear simples da forma
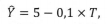
em que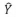 
representa a reta ajustada em função da variável regressora T, tal que 1 < T < 12.
Os erros padrão das estimativas dos coeficientes desse modelo, as razões t e seus respectivos p-valores encontram-se na tabela a seguir
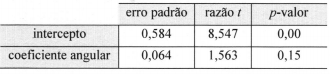
Os desvios padrão amostrais das variáveis Y e T foram, respectivamente, 1 e 3,6.
Com base nessas informações, julgue os itens a seguir.
Um estudo objetivou avaliar a evolução do número mensal Y de milhares de ocorrências de certo tipo de crime em determinado ano. Com base no método dos mínimos quadrados ordinários, esse estudo apresentou um modelo de regressão linear simples da forma
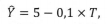
em que representa a reta ajustada em função da variável regressora T, tal que 1 < T < 12.
Os erros padrão das estimativas dos coeficientes desse modelo, as razões t e seus respectivos p-valores encontram-se na tabela a seguir
Os desvios padrão amostrais das variáveis Y e T foram, respectivamente, 1 e 3,6.
Com base nessas informações, julgue os itens a seguir.
Se a média amostrai da variável T for igual a 6,5, então a média amostrai da variável Y será igual a 4,35 mil ocorrências.
Considere duas variáveis aleatórias contínuas, X e Y, tais que P(X > 0) = 1, P(X ≤ 1) = 1/10, P(X ≤ 1|Y > 1) = 3/10, Var(X) = Var(Y) = 1, e Cov(X,Y) = 0.
Com base nessas informações, julgue o item a seguir.
O valor esperado da variável aleatória X é igual a zero.
Com base em uma amostra aleatória simples de tamanho n = 16 retirada de uma população normal com média desconhecida μ e variância a2= 9, deseja-se testar a hipótese nula H1: μ = 0 contra a hipótese alternativa H0: μ ≠ 0 por meio da estatística , na qual denota a média amostral.
Com respeito a esse teste de hipóteses, julgue o item a seguir, sabendo que o valor da média amostral observado na amostra foi igual a 1 e que, relativo a esse teste, o P-valor foi igual a 0,18.
Se o nível de significância escolhido para o teste foi igual a10%, então, nesse caso, a hipótese nula H0:μ = 0 não seria rejeitada, embora a média amostral tenha sido diferente de zero.
Um analista de investimentos acredita que o preço das ações de uma empresa seja afetado pela condição de fluxo de crédito na economia de um certo país. Ele estima que o fluxo de crédito na economia desse país aumente, com probabilidade de 20%. Ele estima também que o preço das ações da empresa suba, com probabilidade de 90%, dentro de um cenário de aumento de fluxo de crédito, e suba, com probabilidade de 40%, sob o cenário contrário.
Uma vez que o preço das ações da empresa subiu, qual é a probabilidade de que o fluxo de crédito da economia tenha também aumentado?
