Considere que X e Y sejam variáveis aleatórias contínuas que se distribuem conjuntamente conforme a função de densidade
f (x, y) = x + y, na qual O <x< 1 e O <y< 1.
Com base nessas informações, julgue o item seguinte
X e Y são variáveis aleatórias independentes.
Um certo sistema anti-incêndio funciona com 3 sensores acoplados de temperatura, de maneira a minimizar as chances de mau funcionamento. O alarme desse sistema soa sempre que grandes variações de temperatura são detectadas por, pelo menos, 2 desses 3 sensores.
Considerando-se que a probabilidade de um sensor não reagir corretamente a uma grande variação de temperatura é 1/5, qual a probabilidade de esse sistema não disparar o alarme em uma situação de grande variação de temperatura?
Após a coleta de dados em um determinado contexto (variáveis A, B, C, … X), uma das formas mais simples e iniciais de análise é a geração e a avaliação de um histograma para uma variável selecionada (ex: X), como por exemplo, em um estudo climático, em que os dados coletados
poderiam incluir a temperatura máxima observada em toda a Terra ao longo de dez anos.
Nesse caso, o histograma adequado é um gráfico em que são apresentadas as
Acerca de bancos de dados relacionais, julgue o item subsequente.
De acordo com a primeira forma normal do modelo relacional, atributos compostos por vários valores são representados diretamente em uma tupla e em suas relações nas tabelas do banco de dados
Determinado pesquisador reuniu dados de vários municípios brasileiros e estimou um modelo de regressão linear múltipla por mínimos quadrados ordinários. A variável dependente foi a taxa de homicídios, e as variáveis independentes incluíam variáveis, como, por exemplo, PIB per capita, média de anos de estudo, índice de Gini e outras variáveis socioeconômicas. Após a estimação, o pesquisador calculou a correlação entre os resíduos e as variáveis independentes e notou que essas correlações foram iguais a zero.
Com referência a essa situação hipotética, julgue o próximo item.
A ausência de correlação entre as variáveis independentes e os resíduos da regressão mostra que as variáveis independentes são exógenas
A tabela apresenta parte da distribuição de frequências das notas de 200 candidatos na primeira fase de um concurso:
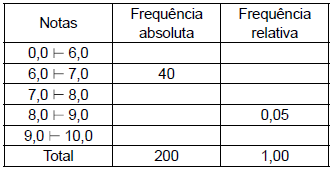
Sabendo-se que 48% dos candidatos tiraram notas maiores ou iguais a 7,0, sendo que a quarta parte deles tiraram notas abaixo de 8,0, é possível afirmar corretamente que, em relação aos 200 candidatos, tiraram notas abaixo de 6,0 ou notas maiores ou iguais a 9,0:
Os alunos de certa escola formaram um grupo de ajuda humanitária e resolveram arrecadar fundos para comprar alimentos não perecíveis. Decidiram, então, fazer uma rifa e venderam 200 tíquetes, numerados de 1 a 200. Uma funcionária da escola resolveu ajudar e comprou 5 tíquetes. Seus números eram 75, 76, 77, 78 e 79. No dia do sorteio da rifa, antes de revelarem o ganhador do prêmio, anunciaram que o número do tíquete sorteado era par.
Considerando essa informação, a funcionária concluiu acertadamente que a probabilidade de ela ser a ganhadora do prêmio era de
Em uma análise financeira, foi modelado que os valores das despesas mensais e das receitas mensais de uma empresa podem, por determinado período, ser descritos pelas funções D(t) e R(t), respectivamente, cujas expressões são dadas a seguir:
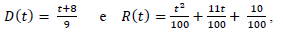
em que t, dado em meses, varia no intervalo [1, 24] e os valores de D(t) e de R(t) são expressos em milhões de reais. Nesse contexto, t = 1 representa o primeiro mês considerado na análise, t = 2 representa o segundo mês e assim sucessivamente. Com base nessas informações, julgue o item seguinte.
Para cada um dos 12 primeiros meses considerados na análise, as despesas mensais foram sempre inferiores a 2,5 milhões de reais.
Em uma análise financeira, foi modelado que os valores das despesas mensais e das receitas mensais de uma empresa podem, por determinado período, ser descritos pelas funções D(t) e R(t), respectivamente, cujas expressões são dadas a seguir:
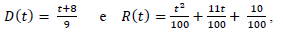
em que t, dado em meses, varia no intervalo [1, 24] e os valores de D(t) e de R(t) são expressos em milhões de reais. Nesse contexto, t = 1 representa o primeiro mês considerado na análise, t = 2 representa o segundo mês e assim sucessivamente. Com base nessas informações, julgue o item seguinte.
De acordo com o modelo formulado, mesmo que as despesas correspondentes ao 15.º mês da análise fossem aumentadas em 40%, o resultado seria inferior às receitas correspondentes a esse mês.
Suponha que o número diário (X) de transações bancárias registradas em determinada conta bancária se distribua conforme uma distribuição de Poisson. Com respeito ao total semanal de transações bancárias registradas nessa conta bancária, denotada como Y = X1 +X2 + X3 +X4 + X5, em que {X1,… , X5} representa uma amostra aleatória simples retirada de uma distribuição de Poisson com média igual a 5 transações por dia, julgue o seguinte item
P(Y=0) = P(X1=0) + P(X2=0) + P(X3=0) + P(X4=0) + P(X5=0) = 5 X e-5
Suponha que o número diário (X) de transações bancárias registradas em determinada conta bancária se distribua conforme uma distribuição de Poisson. Com respeito ao total semanal de transações bancárias registradas nessa conta bancária, denotada como Y= X1 + X2 + X3 + X4 + X5 em que {X1,… , X5} representa uma amostra aleatória simples retirada de uma distribuição de Poisson com média igual a 5 transações por dia, julgue o seguinte item
P(Y=0) = P(X1=0) + P(X2=0) + P(X3=0) + P(X4=0) + P(X5=0) = 5 X e-5
Calcule a probabilidade de se obter soma 9 no lançamento simultâneo de dois dados usuais (seis faces, numeradas de 1 a 6) e não viciados em que o resultado do lançamento foi um número ímpar e um número par:
Considere duas variáveis aleatórias contínuas, X e Y, tais que P(X > 0) = 1, P(X ≤ 1) = 1/10, P(X ≤ 1|Y > 1) = 3/10, Var(X) = Var(Y) = 1, e Cov(X,Y) = 0.
Com base nessas informações, julgue o item a seguir.
X e Y são independentes.
Com base em uma amostra aleatória simples de tamanho n = 16 retirada de uma população normal com média desconhecida μ e variância a2= 9, deseja-se testar a hipótese nula H1: μ = 0 contra a hipótese alternativa H0: μ ≠ 0 por meio da estatística 
, na qual 
denota a média amostral.
Com respeito a esse teste de hipóteses, julgue o item a seguir, sabendo que o valor da média amostral observado na amostra foi igual a 1 e que, relativo a esse teste, o P-valor foi igual a 0,18.
O desvio padrão da média amostral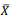 
é igual a 0,75.
Um funcionário de um banco foi incumbido de acompanhar o perfil dos clientes de um determinado produto por meio da Análise de Dados, de forma a aprimorar as atividades de marketing relativas a esse produto. Para isso, ele utilizou a variável classe social desses clientes, coletada
pelo banco, que tem os valores A, B, C, D e E, sem referência a valores contínuos.
Sabendo-se que essa é uma escala ordinal, qual é a medida de tendência central adequada para analisar essa variável?
