Considerando que {zt } representa uma série temporal e que {at} representa uma sequência de choques aleatórios (ruído branco), julgue os itens de 113 a 117, referentes à análise de séries temporais.
Os parâmetros do modelo AR(2), que apresenta os valores
de autocorrelação iguais a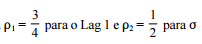 
Lag 2, considerando as equações de Yule-Walker
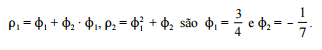
Um analista de órgão público, com o objetivo de verificar se o número de acidentes foi reduzido após a implantação de barreira eletrônica em ponto crítico de uma avenida, realizou uma pesquisa, que consistiu na observação do tráfego de veículos automotores durante 30 horas, divididas uniformemente entre os períodos da manhã, tarde e noite, por meio da qual se constatou a quantidade x de acidentes por hora. Na tabela abaixo, são apresentadas algumas estatísticas descritivas produzidas nessa pesquisa
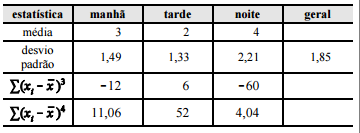
Com base na situação hipotética e na tabela acima apresentadas, julgue os itens a seguir.
Nessa situação, a média geral será igual a três acidentes
por hora.
Um analista de órgão público, com o objetivo de verificar se o número de acidentes foi reduzido após a implantação de barreira eletrônica em ponto crítico de uma avenida, realizou uma pesquisa, que consistiu na observação do tráfego de veículos automotores durante 30 horas, divididas uniformemente entre os períodos da manhã, tarde e noite, por meio da qual se constatou a quantidade x de acidentes por hora. Na tabela abaixo, são apresentadas algumas estatísticas descritivas produzidas nessa pesquisa
Com base na situação hipotética e na tabela acima apresentadas, julgue os itens a seguir.
Nessa situação, de acordo com o momento central de terceira
ordem, a distribuição dos períodos da manhã e da noite será
assimétrica à esquerda.
Considerando que foi realizado estudo para modelar a distribuição da quantidade X de pontos acumulados por infrações de trânsito cometidas por um condutor de veículo de passeio ao longo de um ano, julgue os itens a seguir, relativos a probabilidades e inferência estatística.
Na situação em apreço, considerando-se que X siga uma
distribuição de Poisson com média igual a 10 pontos, é correto
afirmar que a probabilidade de um condutor possuir mais de
20 pontos acumulados será igual a 1 ! 2 P(X < 10).
Considerando que foi realizado estudo para modelar a distribuição da quantidade X de pontos acumulados por infrações de trânsito cometidas por um condutor de veículo de passeio ao longo de um ano, julgue os itens a seguir, relativos a probabilidades e inferência estatística.
Considerando-se a situação em apreço, considerando-se, ainda,
que X siga uma distribuição de Poisson, é correto afirmar que
a média desconhecida 8 poderá ser estimada por intermédio do
método dos momentos, por meio da fórmula
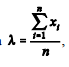
em
que n representa o tamanho da amostra e x1 representa o valor
observado na amostra.
Um engenheiro realizou pesquisa em que analisou a relação entre a quantidade de curvas de um trecho de serra (X) e o tempo gasto em minutos (Y) por veículos de passeio — em que Y seja a variável resposta e X, a variável regressora —, com o objetivo de propor soluções que permitam diminuir o tempo gasto por esses veículos. A tabela abaixo apresenta os resultados da análise de variância (ANOVA) do modelo de regressão linear simples na forma Y = α + βX + g, em que α e β são os coeficientes do modelo e g representa o erro aleatório.
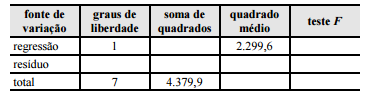
Considerando a situação hipotética e a tabela acima apresentadas, julgue os itens que se seguem
Caso os dados estejam agrupados em classes, a estatística que
deve ser utilizada para medir a correlação entre os dados será
a de Spearman, mas o modelo, apesar disso, deverá ser
estimado por meio da regressão linear simples.
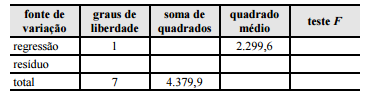
Um engenheiro realizou pesquisa em que analisou a relação entre a quantidade de curvas de um trecho de serra (X) e o tempo gasto em minutos (Y) por veículos de passeio — em que Y seja a variável resposta e X, a variável regressora —, com o objetivo de propor soluções que permitam diminuir o tempo gasto por esses veículos. A tabela abaixo apresenta os resultados da análise de variância (ANOVA) do modelo de regressão linear simples na forma Y = α + βX + g, em que α e β são os coeficientes do modelo e g representa o erro aleatório.
Considerando a situação hipotética e a tabela acima apresentadas, julgue os itens que se seguem
Caso o engenheiro analise a relação inversa — em que X seja
a variável resposta e Y, a variável regressora —, os resultados
do modelo serão exatamente os mesmos.
Um engenheiro realizou pesquisa em que analisou a relação entre a quantidade de curvas de um trecho de serra (X) e o tempo gasto em minutos (Y) por veículos de passeio — em que Y seja a variável resposta e X, a variável regressora —, com o objetivo de propor soluções que permitam diminuir o tempo gasto por esses veículos. A tabela abaixo apresenta os resultados da análise de variância (ANOVA) do modelo de regressão linear simples na forma Y = α + βX + g, em que α e β são os coeficientes do modelo e g representa o erro aleatório.
Considerando a situação hipotética e a tabela acima apresentadas, julgue os itens que se seguem
Dados observacionais produzem os mesmos resultados que
dados experimentais, uma vez que, em ambos os casos, o
pesquisador tem total controle dos erros aleatórios.
Seja a variável aleatória discreta X número de acidentes em um cruzamento registrado em um mês. A probabilidade de que X seja menor ou igual a 2 (ou seja, que ocorram até 2 acidentes no cruzamento em um mês) vale 0,0015.
Qual é a probabilidade de que ocorram mais de 2 acidentes no cruzamento em um mês?
A tabela abaixo apresenta a distribuição de frequências das
idades de um grupo de crianças.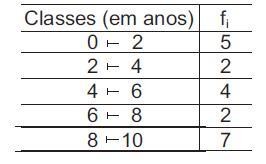
A média das idades dessas crianças, em anos, é
Uma amostra aleatória simples (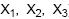
) provém de uma população normalmente distribuída com média ? e variância unitária. Entre os estimadores de ? (Y) da classe Y = (m + 1)
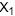+ (m ? 2)
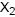+ 2(1 ? m)
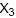, sendo m um parâmetro real, o mais eficiente será no caso em que m for igual a
Um estudo realizado em uma fábrica determinou que o intervalo de confiança de 90% para a vida média dos equipamentos, em horas, foi [891,80; 908,20]. Para esta conclusão, considerou-se a população normalmente distribuída, de tamanho infinito e uma amostra aleatória de 64 equipamentos. Se, na distribuição normal padrão (Z), a probabilidade P(Z > 1,64) = 5%, então, o desvio padrão populacional, em horas, desta população é igual a
Para resolver as questões de números 42 e 43
considere que foi obtido, por meio do método dos
mínimos quadrados, o ajustamento do modelo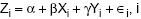
= 1, 2, 3, . . . , em que i corresponde
a i-ésima observação, ?, ? e ? são
parâmetros desconhecidos e 
o erro aleatório, com
as respectivas hipóteses consideradas para a regressão
linear múltipla. Uma amostra aleatória com 35
observações (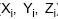
) foi utilizada, obtendo-se os
valores de 1,5 e 3,0 para as estimativas de ? e ?,
respectivamente.
Considerando a equação do plano obtida pelo método dos mínimos quadrados, se X = 8 e Y = 20, o valor estimado de Z será
Em um lote de 8 peças há duas defeituosas e 6 boas. Escolhendo-se ao acaso e sem reposição 3 peças do lote, a probabilidade de se encontrar no máximo uma defeituosa é
Para o modelo ARMA (1,1) dado por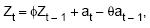
onde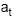 
é o ruído branco de média zero e variância ?2, considere as seguintes afirmações:
I. as condições de estacionariedade e invertibilidade do modelo são dadas respectivamente por: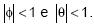 
II. para qualquer valor do parâmetro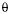 
o modelo é invertível.
III. as condições de estacionariedade e invertibilidade do modelo são dadas respectivamente por: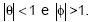 
IV. a função de autocorrelação de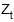 
decai exponencialmente após o lag 1.
É correto o que consta APENAS em
