De uma distribuição com média 100 e variância 25 são coletados 225 valores independentes (amostra). Denotando-se a média amostral por M e considerando a aproximação
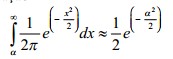
a probabilidade de que |M-80| < 1 é
Assinale a alternativa que apresenta uma propriedade desejável de um bom estimador.
De acordo com a literatura especializada, o bom uso de um teste diagnóstico requer, além de considerações clínicas, o conhecimento de medidas que caracterizam sua qualidade intrínseca: a sensibilidade, a especificidade e os parâmetros que refletem sua capacidade de produzir decisões clínicas corretas – valor da predição positiva (VPP) e valor da predição negativa (VPN). A sensibilidade, denotada por s, é definida como s = P[T+|D+]. Já a especificidade, denotada por e, é definida como e = P[T–|D–]. A sensibilidade e a especificidade, embora sejam bons sintetizadores das qualidades de um teste, não auxiliam na decisão da equipe médica que, recebendo um paciente com resultado positivo do teste, precisa avaliar se o paciente está ou não doente. Daí a necessidade do VPP e VPN. Sendo, então, p = P(D+) a prevalência da doença na população de interesse, isto é, a proporção de pessoas doentes, ou a probabilidade de doença pré-teste, assinale a alternativa correta que corresponde à expressão que leva ao cálculo do valor da predição positiva (VPP).
Uma variável aleatória X tem distribuição normal, com média 100 e desvio padrão 10. Se
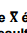
é a média de uma amostra
com 25 elementos selecionados dessa população e o interesse é
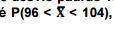
o resultado para a probabilidade
desejada é:
Considere um modelo de regressão linear simples, em que β0 = 5, β1 = 2,5 e ? com distribuição normal com média 0 e variância 3. Assinale a alternativa que indica a distribuição de Y quando X = 2

Um processo estocástico {X(t); t ≥ 0} será chamado de Processo de Contagem se
Testes não paramétricos são comumente utilizados quando
No conjunto de números: 4; 6; 7; 9; 10, é correto afirmar
que o valor do segundo momento é:
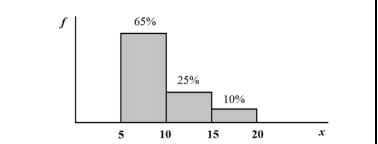
Com referência à figura acima, que mostra a distribuição da renda
mensal — x, em quantidades de salários mínimos (sm) — das
pessoas que residem em determinada região, julgue os itens
subsequentes.
A mediana da variável x é superior a 8 sm e inferior a 9 sm.
As quantidades diárias de processos administrativos (N )
protocolados em certo órgão público seguem uma distribuição de
Poisson com média igual a 5. Cada processo protocolado é
encaminhado para a superintendência A ou para a B e, assim, a soma
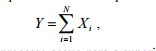
em que Xi = 1 se o processo segue para a superintendência A, e Xi = 0 se o processo segue para B, representa o total diário de
processos administrativos protocolados que se destinam para a
superintendência A.
Com base nessa situação, julgue os seguintes itens considerando
que X1, X2, ..., XN sejam variáveis aleatórias independentes, e que
P(X1 = 1) = P(X2 = 1) = ... = P(XN = 1) = 0,8.
O número diário de processos protocolados que são destinados à superintendência B segue uma distribuição de Poisson com média igual a 1.
As quantidades diárias de processos administrativos (N )
protocolados em certo órgão público seguem uma distribuição de
Poisson com média igual a 5. Cada processo protocolado é
encaminhado para a superintendência A ou para a B e, assim, a soma
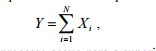
em que Xi = 1 se o processo segue para a superintendência A, e Xi = 0 se o processo segue para B, representa o total diário de
processos administrativos protocolados que se destinam para a
superintendência A.
Com base nessa situação, julgue os seguintes itens considerando
que X1, X2, ..., XN sejam variáveis aleatórias independentes, e que
P(X1 = 1) = P(X2 = 1) = ... = P(XN = 1) = 0,8.
A quantidade média diária de processos administrativos que se destinam para a superintendência A é igual a 4.
Considerando a função de densidade conjunta na forma f(x, y) = c,
em que 0 < x < y < 1 e c > 0 é uma constante de normalização,
julgue os seguintes itens.
A constante de normalização é inferior ou igual a 1.
Considere que a amostra aleatória simples X1, X2, ..., Xn tenha sido
retirada de uma distribuição exponencial com função de densidade
na forma f(x) = γexp(–γx), em que x > 0 e γ > 0. Com relação a essa
amostra e à inferência estatística, julgue os itens que se seguem.
Considere que T(X1, X2, ..., Xn) seja o estimador do tipo UMVUE (uniformly minimum-variance unbiased estimator) de γ. Nessa situação, a variância da estatística T(X1, X2, ..., Xn) corresponde ao limite inferior de Cramer-Rao.
Julgue os itens seguintes, relativos às técnicas de amostragem
Suponha que um caso polêmico esteja sendo julgado por um tribunal e que, para avaliar a proporção de pessoas na população favoráveis ao resultado positivo nesse processo, o tribunal decida fazer uma enquete. Nesse caso, para se calcular o tamanho da amostra que responderá à enquete, será necessário conhecer o tamanho da população.

