Uma esfera está mergulhada em um tanque com formato cilíndrico. O volume restante no tanque está completamente preenchido com água, como ilustra a figura.
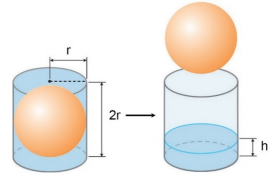
O raio, tanto da esfera como do cilindro, é r, e a altura do cilindro é de 2r. Se a esfera for retirada do tanque, como indicado na figura, a altura h, do nível da água, corresponderá a que fração da altura do cilindro?
Considere um recipiente com a forma de paralelepípedo reto retângulo e com dimensões, em centímetros, indicadas na figura.
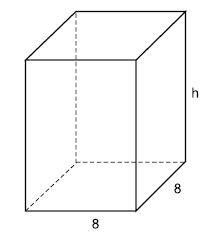
Se colocarmos 576 cm3 de um líquido nesse recipiente, inicialmente vazio, a quarta parte da sua capacidade total não será preenchida. Nessas condições, é correto afirmar que a medida da altura desse recipiente, indicada por h na figura, é
A altura do cone de revolução circunscrito a uma esfera de raio R, dado o volume do cone igual a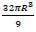 
é:
Um reservatório de água tem a parte interna em formato de paralelepípedo reto retangular, altura de 1 metro, base retangular, e capacidade para 5 000 litros de água, o que corresponde a 5 m3. Necessita-se construir outro reservatório, no mesmo formato do reservatório descrito, com a mesma altura interna, mas com a área da base medindo oitenta e um centésimos da área daquele reservatório, de modo que a maior aresta da base tenha o quíntuplo da medida da menor. Dessa forma, a medida da menor aresta da base do novo reservatório deverá ser de
Considere um cilindro oco de volume V. A razão entre a área da base e a área da superfície lateral, de modo que a quantidade de material usado para produzi-lo seja o mínimo possível, é
Uma pirâmide regular, de base quadrada, tem altura igual a 10cm e 30cm3 de volume. Constrói-se um cubo de aresta igual à aresta da base dessa pirâmide. Então, o volume do cubo é _____cm3.
Muitos restaurantes servem refrigerantes em copos contendo limão e gelo. Suponha um copo de formato cilíndrico, com as seguintes medidas: diâmetro = 6 cm e altura = 15 cm. Nesse copo, há três cubos de gelo, cujas arestas medem 2 cm cada, e duas rodelas cilíndricas de limão, com 4 cm de diâmetro e 0,5 cm de espessura cada. Considere que, ao colocar o refrigerante no copo, os cubos de gelo e os limões ficarão totalmente imersos. (Use 3 como aproximação para π).
O volume máximo de refrigerante, em centímetro cúbico, que cabe nesse copo contendo as rodelas de limão e os cubos de gelo com suas dimensões inalteradas, é igual a
Um mestre de obras deseja fazer uma laje com espessura de 5 cm utilizando concreto usinado, conforme as dimensões do projeto dadas na figura. O concreto para fazer a laje será fornecido por uma usina que utiliza caminhões com capacidades máximas de 2 m3, 5 m3 e 10 m3 de concreto.
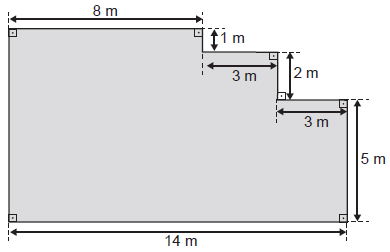
Qual a menor quantidade de caminhões, utilizando suas capacidades máximas, que o mestre de obras deverá pedir à usina de concreto para fazer a laje?
Um pedaço retangular de papel tem 50 cm de perímetro, e a medida do seu comprimento tem 5 cm a mais do que a medida da sua largura, conforme indica a figura, cujas medidas indicadas estão em centímetros.
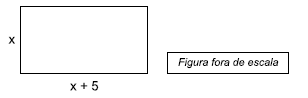
Esse pedaço de papel foi recortado e somente a medida de seu comprimento foi reduzida em 2 cm. A medida do comprimento após a redução passou a ser de
Uma formiga encontra-se no ponto X, no lado externo de um copo que tem a forma de um cilindro reto. No lado interno, no ponto V, existe um grão de açúcar preso na parede do copo. A formiga segue o caminho XYZWV (sempre sobre a superfície lateral do copo), de tal forma que os trechos ZW e WV são realizados na superfície interna do copo. O caminho XYZWV é mostrado na figura.
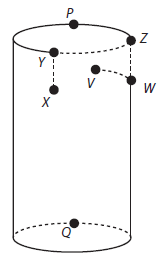Sabe-se que: os pontos X, V, W se encontram à mesma distância da borda; o trajeto WV é o mais curto possível; os trajetos XY e ZW são perpendiculares à borda do copo; e os pontos X e V se encontram diametralmente opostos.
Supondo que o copo é de material recortável, realiza-se um corte pelo segmento unindo P a Q, perpendicular à borda do copo, e recorta-se também sua base, obtendo então uma figura plana. Desconsidere a espessura do copo.
Considerando apenas a planificação da superfície lateral do copo, a trajetória da formiga é
Para decorar sua casa, uma pessoa comprou um vaso de vidro em forma de um paralelepípedo retangular, cujas medidas internas são: 40 cm de comprimento, 35 cm de largura e 60 cm de altura. Em seguida, foi até uma floricultura e escolheu uma planta aquática para colocar nesse vaso. Segundo uma proposta do gerente do local, essa pessoa avaliou a possibilidade
de enfeitar o vaso colocando uma certa quantidade de pedrinhas artificiais brancas, de volume igual a 100 cm3 cada uma delas, que ficarão totalmente imersas na água que será colocada no vaso. O gerente alertou que seria adequado, em função da planta escolhida, que metade do volume do vaso fosse preenchido com água e que, após as pedrinhas colocadas, a altura da água deveria ficar a 10 cm do topo do vaso, dando um razoável espaço para o crescimento da planta. A pessoa aceitou
as sugestões apresentadas, adquirindo, além da planta, uma quantidade mínima de pedrinhas, satisfazendo as indicações do gerente.
Nas condições apresentadas, a quantidade de pedrinhas compradas foi
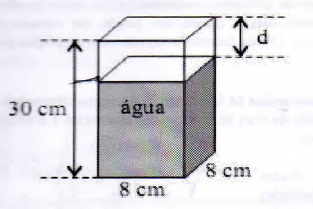
Uma jarra de fundo quadrado, medindo 8 cm de lado e 30 cm de altura estava inicialmente cheia de água até sua borda superior, mas foram descartadas 5 canecas com 64 ml de água cada, fazendo com que a jarra diminuísse seu nível de água, conforme mostra a figura acima. A distância d, em cm, entre o nível da água que restou na jarra e a borda superior é:
Sabe-se que o volume de um cone reto corresponde à terça parte do volume de um cilindro reto de mesma base e mesma altura. Uma peça maciça de vidro é constituída de um cilindro reto de altura 10 cm, cujo raio da base mede 2 cm, vazado por uma região cônica reta com a mesma base do cilindro e altura 6 cm. Observa-se, na figura, que a parte maciça da peça, em vidro, é a região pintada.
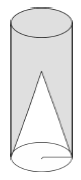
Adotando π = 3, o volume de vidro da peça é, em centímetros cúbicos, igual a:
Mário pretende ampliar um reservatório em forma de paralelepípedo de sua casa no qual tem volume 48m³. Porém ele esqueceu duas das medidas do volume, mas ele sabe que o comprimento mede x metros, a largura mede x-4 metros e a altura mede 4 metros. A soma do comprimento, da largura e da altura do paralelepípedo é:
Tonel é um recipiente utilizado para armazenar líquidos. Uma vinícola utiliza tonéis com capacidade de 1 000 litros cada um, para armazenar sua produção de 50 m3 de vinho.
Quantos tonéis serão necessários para armazenar toda a produção dessa vinícola?
