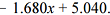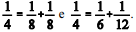Se a > 0 e ln
a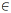 
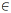
[10, 20), então ln a2 
[100, +∞).
Cada j = 0, 1, …, 11 representa um mês do ano de 2017, isto é, j = 0 = janeiro, j = 1 = fevereiro, e assim sucessivamente. Se o mês j tem d dias, então j + 1/d representa o dia 1.º do mês j; j + 2/d representa o dia 2 do mês j, e assim sucessivamente, j + d/d = j + 1 representa o dia d do mês j. Dessa forma, cada dia do ano de 2017 pode ser representado por um número x do intervalo [0, 12]. Considere que, nessa representação, em cada dia x do ano de 2017, a porcentagem de água acumulada em relação à capacidade máxima do reservatório de determinada represa seja expressa pelo valor da função f(x) = x2 - 10x + 60.
A partir dessas informações, julgue o item que se segue.
Sabendo-se que fevereiro de 2017 teve 28 dias, então f(1,25) é a porcentagem de água acumulada no reservatório da represa no dia 25/2/2017.
Cada j = 0, 1, …, 11 representa um mês do ano de 2017, isto é, j = 0 = janeiro, j = 1 = fevereiro, e assim sucessivamente. Se o mês j tem d dias, então j + 1/d representa o dia 1.º do mês j; j + 2/d representa o dia 2 do mês j, e assim sucessivamente, j + d/d = j + 1 representa o dia d do mês j. Dessa forma, cada dia do ano de 2017 pode ser representado por um número x do intervalo [0, 12]. Considere que, nessa representação, em cada dia x do ano de 2017, a porcentagem de água acumulada em relação à capacidade máxima do reservatório de determinada represa seja expressa pelo valor da função f(x) = x² - 10x + 60.
A partir dessas informações, julgue o item que se segue.
Se, para 2018, a previsão para a porcentagem de água no reservatório for dada pela composição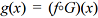 
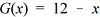
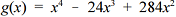
, em que 
, então 
A figura seguinte mostra, em um sistema de coordenadas cartesianas ortogonais xOy, em que a unidade de medida é o metro, uma região retangular OABC. O lado OA mede 600 m e o lado OC mede 800 m.
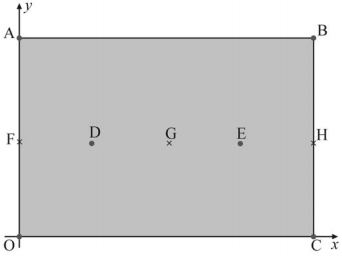
A figura mostra também os pontos F = ponto médio de OA, H = ponto médio de CB, G = centro do retângulo OABC, D = ponto médio de FG, e E = ponto médio de GH. Nos pontos O, A, B, C, D e E foram instalados pontos de acesso à Internet — wi-fi. Nessa configuração, o usuário consegue se conectar à Internet desde que o seu smartphone esteja a 200 m ou menos de qualquer desses pontos de acesso.
Com base nessas informações e na figura apresentada, julgue o próximo item.
Se um smartphone está em um drone, a 50 m de altura sobre o ponto P = (100, 100), então, nesse caso, é possível conectá-lo à Internet a partir do ponto de acesso localizado na origem O.
Com relação a uma sequência numérica a 1, a2, …, an, julgue o item subsequente.
Se a sequência estiver em progressão aritmética com razão igual a 10 e a 1 = 5, então a10 > 100.
A respeito dos números complexos, julgue o item a seguir.
Se q é um número real diferente de zero e se ω é uma das raízes da equação zn = q, então as raízes dessa equação são: q1/n; ω; ω2; …; ωn-1.
Julgue o item que se segue, relativo a matrizes e sistemas lineares.
Um sistema linear escrito na forma matricial PX = -X, em que P é uma matriz n × n de coeficientes constantes e X é a matriz das incógnitas, n × 1, tem solução única se, e somente se, a matriz P + I for inversível (I é a matriz identidade n × n).
A respeito de história da matemática, julgue o item subsequente.
Em virtude de necessidades contábeis da época, os egípcios tinham a preferência pela utilização das frações unitárias, isto é, aquelas em que o número 1 é o numerador. Parte do Papiro de Rhind, um importante registro matemático dos egípcios, trata da decomposição de frações a partir de frações unitárias. As frações unitárias na forma 1/n sempre podem ser decompostas em exatamente duas frações unitárias, por exemplo,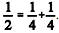 
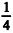
Nesse contexto, é correto afirmar que as únicas decomposições da fração unitária 
são 
Tendo como referência inicial as informações apresentadas no texto precedente, é correto afirmar que a avaliação formativa
tende a funcionar melhor quando o professor evita práticas de classificação bem como comentários que comparem o desempenho dos alunos.
Tendo como referência inicial as informações apresentadas no texto precedente, é correto afirmar que a avaliação formativa
deve ser desenvolvida em contexto e integrada aos processos de ensino, com a participação ativa dos alunos.
Considerando o texto apresentado e os múltiplos aspectos a ele relacionados, julgue o próximo item, com relação ao uso da resolução de problemas nas atividades avaliativas.
A resolução de problemas possibilita a avaliação de aspectos originais e criativos do pensamento dos alunos.
Ainda a respeito das competências e habilidades propostas pelos Parâmetros Curriculares Nacionais do Ensino Médio para a disciplina de matemática, julgue o próximo item.
Nos parâmetros curriculares nacionais do ensino médio, os temas que serão estudados e possibilitarão o desenvolvimento das competências e habilidades almejadas são divididos em apenas dois grandes eixos: álgebra e geometria.
O número de Euler, nome dado em homenagem ao matemático suíço Leonhard Euler, é um número irracional denotado por e, cuja representação decimal tem seus 4 primeiros algarismos dados por 2,718. Esse número é a base dos logaritmos naturais, cuja função f(x) = lnx = logex tem inúmeras aplicações científicas.
A respeito desse assunto, julgue o item a seguir.
Se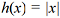 
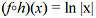
é a função módulo, então o domínio da função composta 
é o conjunto dos números reais.
Cada j = 0, 1, …, 11 representa um mês do ano de 2017, isto é, j = 0 = janeiro, j = 1 = fevereiro, e assim sucessivamente. Se o mês j tem d dias, então j + 1/d representa o dia 1.º do mês j; j + 2/d representa o dia 2 do mês j, e assim sucessivamente, j + d/d = j + 1 representa o dia d do mês j. Dessa forma, cada dia do ano de 2017 pode ser representado por um número x do intervalo [0, 12]. Considere que, nessa representação, em cada dia x do ano de 2017, a porcentagem de água acumulada em relação à capacidade máxima do reservatório de determinada represa seja expressa pelo valor da função f(x) = x2 - 10x + 60.
A partir dessas informações, julgue o item que se segue.
A diferença entre os percentuais de água contida na represa em 31/12/2017 e 1.º/1/2017 é superior a 20%.
Cada j = 0, 1, …, 11 representa um mês do ano de 2017, isto é, j = 0 = janeiro, j = 1 = fevereiro, e assim sucessivamente. Se o mês j tem d dias, então j + 1/d representa o dia 1.º do mês j; j + 2/d representa o dia 2 do mês j, e assim sucessivamente, j + d/d = j + 1 representa o dia d do mês j. Dessa forma, cada dia do ano de 2017 pode ser representado por um número x do intervalo [0, 12]. Considere que, nessa representação, em cada dia x do ano de 2017, a porcentagem de água acumulada em relação à capacidade máxima do reservatório de determinada represa seja expressa pelo valor da função f(x) = x2 - 10x + 60.
A partir dessas informações, julgue o item que se segue.
Em 2017, a quantidade de água acumulada no reservatório ficou acima de 51% de sua capacidade máxima em dias de exatamente 4 meses.
