Na tabela a seguir, estão apresentados os salários pagos em um estabelecimento comercial e a quantidade de funcionários que recebe esses salários.
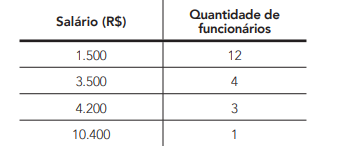
A média e a mediana desses salários são, em reais, respectivamente, iguais a:
Considere o seguinte sistema de equações lineares, sendo k uma constante real.
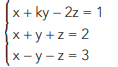
Se esse sistema apresenta uma única solução, o conjunto de todos os valores reais que a constante k pode assumir é:
Ao finalizar o 6º nível em um jogo eletrônico, Valdomiro conquistou um total de 420.784 pontos. A tabela a seguir mostra a quantidade de pontos obtidos nos 5 níveis iniciais:

O total de pontos obtidos no 6º nível é igual a:
Em uma equipe composta por seis colaboradores de uma obra, é necessário selecionar três deles para desempenhar três tarefas distintas, sendo que cada tarefa deve ser realizada por apenas um colaborador. O total de maneiras diferentes de selecionar esses colaboradores é igual a
O soldado Arquimedes precisa encher de água um recipiente com capacidade de 80 litros e dispõe de um vasilhame cujo formato é
um paralelepípedo com base quadrada de lado 15 cm e 18 cm de altura. Arquimedes deverá encher o vasilhame em uma bica e
despejar a água no recipiente.
Para encher o recipiente, o número de vezes que Arquimedes deverá encher e despejar a água do vasilhame no recipiente é igual a
Uma hamburgueria oferece dois tipos de hambúrgueres: clássico e premium. Um hambúrguer premium é 25% mais caro quando comparado a um hambúrguer clássico. Além disso, um suco de laranja custa a metade do valor de um hambúrguer premium.Um hambúrguer clássico, um hambúrguer premium e dois sucos de laranja custam, juntos, R$ 84,00.Com base nessas informações, é correto concluir que a diferença entre os preços de um hambúrguer premium e de um hambúrguer clássico é de
Representada sobre um plano cartesiano, uma reta
A média aritmética de 4 números inteiros positivos é 9. A mediana da lista formada por eles vale 8.
Se a diferença entre o maior e o menor desses números é igual a 10, então o maior deles é
Um bombeiro precisa cortar uma barra de ferro de 0,0036 km em pedaços de 15 cm cada. Quantos pedaços ele conseguirá obter com essa barra de ferro?
Analise a seguinte sequência numérica: 84; 87; 90; 93; ...
Seguindo o padrão de formação da sequência, o décimo primeiro termo será:
Uma pesquisa com pessoas consideradas bem-sucedidas buscou identificar a prática de três hábitos relacionados ao estilo de vida: acordar cedo; ler com frequência; e fazer exercícios físicos regularmente. Os resultados obtidos foram os seguintes:
• 34 pessoas acordam cedo;
• 55 pessoas leem com frequência;
• 21 pessoas fazem exercícios físicos regularmente;
• 8 pessoas possuem os três hábitos;
• 21 pessoas acordam cedo e leem com frequência;
• 13 pessoas acordam cedo e fazem exercícios físicos;
• 11 pessoas leem com frequência e fazem exercícios físicos; e
• 2 pessoas não possuem nenhum dos três hábitos.
Com base nessa situação hipotética, julgue o item a seguir.
Selecionando-se aleatoriamente uma pessoa entre aquelas que fazem exercícios físicos regularmente e praticam mais de um dos hábitos investigados, a probabilidade de ela também acordar cedo e de ler com frequência é superior a 50%.
Ana, Beatriz e Cecília são grandes fãs de filmes de terror de baixo orçamento e estão eufóricas para assistir ao lançamento de A Geladeira Assassina 3: o degelo final. Antes de entrar no cinema, viram uma pesquisa feita com pessoas que já tinham assistido aos três filmes da trilogia. Nessa pesquisa, cada pessoa pôde escolher apenas um dos filmes como seu favorito: o primeiro (A Geladeira Assassina), o segundo (A Geladeira Assassina 2: gelo em dobro) ou o terceiro filme da franquia. Os resultados foram os seguintes:
• 35% das pessoas disseram que o favorito era o primeiro filme;
• 30 pessoas preferiram o segundo; e
• 48 pessoas escolheram o terceiro como o melhor.
Com base nessa situação hipotética, julgue os itens a seguir.
O número total de pessoas entrevistadas foi igual a 120.
A professora Isabel propôs uma atividade para seus alunos usando os dias da semana em português e em espanhol. Ela escreveu dois conjuntos: o conjunto A, com os dias da semana em português, é A = {segunda-feira, terça-feira, quarta-feira, quinta-feira, sexta-feira, sábado, domingo}; e o conjunto B, com os dias da semana em espanhol, é B = {lunes, martes, miércoles, jueves, viernes, sábado, domingo}. Com base nessa situação hipotética e nos conjuntos apresentados, julgue os itens a seguir.
A diferença entre o conjunto A e o conjunto B é um conjunto vazio.
A professora Isabel propôs uma atividade para seus alunos usando os dias da semana em português e em espanhol. Ela escreveu dois conjuntos: o conjunto A, com os dias da semana em português, é A = {segunda-feira, terça-feira, quarta-feira, quinta-feira, sexta-feira, sábado, domingo}; e o conjunto B, com os dias da semana em espanhol, é B = {lunes, martes, miércoles, jueves, viernes, sábado, domingo}. Com base nessa situação hipotética e nos conjuntos apresentados, julgue os itens a seguir.
A interseção entre os conjuntos A e B tem exatamente dois elementos.
Rosilene faz flexões todo dia ao acordar. A tabela a seguir mostra o número de flexões que Rosilene fez em cada dia de uma determinada semana.
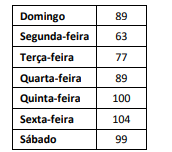
Nessa semana, o número de dias em que Rosilene fez mais flexões do que a média da semana foi

