Um número inteiro positivo N, de 2 algarismos, é tal que exatamente 3 das 4 afirmações a seguir são verdadeiras:
- N é um número par;
- N é um número primo;
- N é um múltiplo de 3;
- um dos algarismos de N é 5.
O algarismo das unidades de N é
Em um campeonato de futebol de turno único com 10 times, cada time joga uma única vez com cada um dos outros 9. Cada vitória vale 3 pontos, cada empate vale 1 ponto e cada derrota vale 0 (zero) ponto. Ao final, 3 times acabaram empatados (mesmo número total de pontos) em primeiro lugar.
Assinale a opção que indica o número máximo de pontos que cada um desses 3 times fez.
Maria quer cortar uma corda em 6 pedaços de mesmo tamanho e marca os pontos onde deverá efetuar os cortes. José quer cortar a mesma corda em 8 pedaços de mesmo tamanho e também marca os pontos onde a corda deve ser cortada. Carlos corta a corda em todos os pontos marcados por Maria e José. O número de pedaços de corda resultante é:
Uma loja anuncia uma geladeira cujo preço à vista é de R$ 3.500,00. Não dispondo deste capital, um cliente sepropõe a pagar a geladeira, com juros compostos de 4% a.m., em quatro prestações mensais, de mesmo valor, sendo a primeira no ato da compra.
Qual o valor aproximado da prestação que o cliente está se propondo a pagar em reais?
No que diz respeito à relação professor-estudante no ambiente educativo, julgue o item subsecutivo.
A função docente requer um distanciamento emocional que garanta a autoridade do professor no contexto da sala de aula.
Num caminhão do corpo de Bombeiros, a manutenção dos equipamentos é feita da seguinte forma: Escada: a cada dois dias. Extintores: a cada três dias. Mangueiras: a cada cinco dias. Hoje, todos esses equipamentos estão sendo revisados ao mesmo tempo. Podemos afirmar que isso irá ocorrer novamente em_______ dias.
Assinale a alternativa que preenche corretamente a lacuna.
Uma organização adota sistema de reposição contínua para seu estoque de determinado insumo. O consumo mensal do insumo é de 150 unidades em média e o estoque de segurança é de 40 unidades. As aquisições são realizadas por compra direta aos fornecedores, o custo de pedido é de R$ 25,00 e o tempo de ressuprimento é de 15 dias corridos.
Na situação descrita, o ponto de pedido é (considere que um mês tem 30 dias):
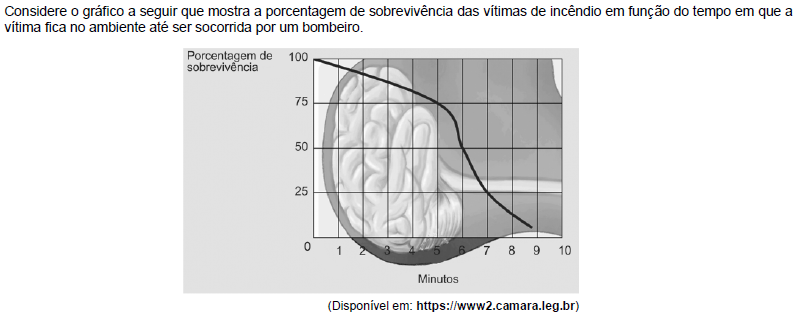
De acordo com o gráfico, do 5o ao 7o minuto as chances de sobrevivência de uma vítima de incêndio diminuem em cerca de
Ao colocar todos os anagramas da palavra COPA em ordem alfabética, como em um dicionário, em qual posição aparece a palavra AOCP?
Raquel começou a escrever em seu caderno os números inteiros e positivos, 1, 2, 3, ..., e parou quando escreveu o milésimo algarismo. Os três últimos algarismos que Raquel escreveu foram:
Em uma prova de Matemática, o professor apresentou a seguinte questão: “Considere os polinômios P(x) = (x + 1)6 e Q(x) = x6. Sabendo-se que P(x) = Q(x), encontre a soma S de todos os valores de x reais que satisfazem a igualdade. Justifique o raciocínio utilizado”. A seguir, são apresentadas as respostas de quatro alunos:
Aluno A: Extraindo a raiz sexta em ambos os membros, tem-se que x+1 = x. Conclui-se que não existe x que satisfaça a equação e, portanto, S é o conjunto vazio.
Aluno B: Observando a equação dada, verifica-se que x = -1/2 é raiz da equação. Como a equação é do sexto grau, S = 6.(-1/2), ou seja, S = -3.
Aluno C: A equação (x + 1)6 = x6 é equivalente a (x + 1)6 – x6 = 0. Fatorando corretamente o primeiro membro da equação, obtém-se uma equação polinomial do 5º grau, cujas raízes são a, b, c, d e e, sendo a = -1/2, b e c complexos conjugados e d e e complexos conjugados, cujas partes reais são -1/2. Assim, S = -3.
Aluno D: A equação (x + 1)6 = x6 é equivalente a (x + 1)6 - x6 = 0. Fatorando corretamente o primeiro membro da equação, obtém-se uma equação polinomial do 5º grau, cujas raízes são a, b, c, d e e, sendo a = -1/2, b e c complexos conjugados e d e e complexos conjugados, cujas partes reais são -1/2. Assim, S = -5/2.
Diante do exposto, analise as assertivas a seguir e assinale a alternativa que aponta as corretas.
I. O aluno A apresentou uma justificativa incorreta e o valor incorreto de S.
II. O aluno B apresentou uma justificativa incorreta, mas o valor correto de S.
III. O aluno C apresentou uma justificativa correta e o valor incorreto de S.
IV. O aluno D apresentou uma justificativa correta e o valor correto de S.
Sobre Geometria Espacial: de posição e métrica, assinale a alternativa correta.
Seja
No plano cartesiano temos um quadrado ABCD e três retas paralelas, s, r e t. Os vértices A, C e D pertencem, respectivamente, às retas t, s e r, como na figura abaixo.

A distância entre as retas s e r é 3 e entre r e t é 7. A área do quadrado ABCD é:
Em um baralho convencional de 52 cartas, desejamos escolher quatro cartas. Sem levarmos em consideração a ordem delas, queremos que em cada escolha haja pelo menos uma dama. De quantas formas podemos escolher essas quatro cartas?