Alfredo, que é um bom aluno, tem um acordo com o pai: se ele mantiver as notas altas, recebe aumento de 10% na mesada a cada mês. Sabe-se que a mesada inicial de Alfredo era de R$100,00.
Considerando que Alfredo manteve as notas altas durante todo o ano letivo, o valor da mesada após o terceiro mês será:
Em uma loja de doces, 2 barras de chocolate e 5 bombons custam R$ 39,00 e 3 barras de chocolate e 3 bombons custam R$ 45,00. Com essas informações, podemos dizer que 1 barra de chocolate e 2 bombons custam:
A média das idades dos funcionários de uma empresa é igual a 44 anos. No próximo mês, 5 funcionários irão se aposentar, sendo que um tem 64 anos, dois têm 65 anos e dois têm 69 anos. Para substituí-los, serão contratados 8 pessoas, cujas idades têm média igual a 28 anos. Sabendo que os atuais funcionários e os futuros contratados já fizeram aniversário esse ano, e que, após a substituição de todos os envolvidos, a nova média das idades dos funcionários dessa empresa será igual a 42 anos, o número atual de funcionários da empresa é
A tabela a seguir apresenta os números de filhos de alguns funcionários de uma empresa, sendo que alguns valores são desconhecidos:
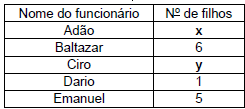
Sabe-se que Adão tem 2 filhos a mais que Ciro; e que, se for calculada a média aritmética simples dos números de filhos levando-se em conta os 5 funcionários, será obtido o valor médio de 4 filhos por funcionário. Então, é correto afirmar que y é igual a
A seguir, são apresentadas informações obtidas a partir de uma pesquisa realizada com 1.000 pessoas.
• 480 possuem plano de previdência privada;
• 650 possuem aplicações em outros tipos de produtos financeiros;
• 320 não possuem aplicação em nenhum produto financeiro.
Com base nessa situação hipotética, julgue o item seguinte.
Se uma pessoa escolhida ao acaso entre as que participaram da pesquisa possui plano de previdência privada, então a probabilidade de ela possuir também aplicação em outros produtos financeiros é superior a 90%.
Quanto a equações e inequações de 1.º e 2.º graus, julgue o próximo item.
Para o conjunto o maior número inteiro é x = 4.
Uma caixa contém 4 bolas numeradas 1, 2, 3 e 4. Selecionam-se, ao acaso, 2 bolas sem reposição.
A probabilidade de 3 ser o maior número selecionado é
Uma caixa com o formato de um paralelepípedo tem dimensões iguais a 25 cm, 36 cm e 20 cm.
A capacidade volumétrica dessa caixa, em litros, é
As medidas em graus dos 3 ângulos internos de um triângulo são diretamente proporcionais a 3, 4 e 5, respectivamente.
O maior ângulo desse triângulo mede, em graus:
Para a pintura externa de um prédio foram contratados pintores no regime de trabalho de 6 horas por dia.
Sabe-se que 5 desses pintores realizam a pintura em exatamente 10 dias inteiros de trabalho.
Se apenas 3 pintores forem contratados no mesmo regime de trabalho, o tempo que levarão para concluir a pintura é de
As idades das quatro primas Fernanda, Gláucia, Helena e Íris são 13, 18, 22 e 24, embora não necessariamente nessa ordem.
Fernanda é mais nova do que Helena. A soma das idades de Íris e Fernanda é divisível por 5. A soma das idades de Íris e Helena também é divisível por 5.
A soma das idades de Fernanda e Gláucia é
Em um consultório dentário anota-se diariamente o nome do paciente, o horário de início e término de cada consulta.
A tabela a seguir mostra as consultas realizadas em um dia.
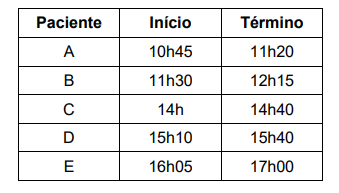
O tempo médio, em minutos, de uma consulta foi
Os 3 primeiros colocados de uma corrida de rua dividiram um prêmio de R$ 7.685,00. O valor individual recebido foi calculado por meio de divisão em partes inversamente proporcionais ao tempo de corrida de cada corredor. O terceiro colocado, corredor que fez o maior tempo, recebeu R$ 2.030,00 e o tempo do segundo colocado corresponde a sete sextos do tempo do vencedor da corrida.
O valor recebido pelo vencedor dessa corrida foi
Os números 1, 2, 3, 4, 5, 6 e 7 devem ser divididos em dois grupos de forma que a soma dos números de cada grupo seja a mesma.
O número de maneiras distintas para fazer isso é
No futebol, para a cobrança de uma falta, a barreira deve ficar a 10 jardas da bola segundo a regra oficial. Sabe-se que 1 jarda é
equivalente a 3 pés, que 1 pé equivale a 12 polegadas e que uma polegada é equivalente a 2,54 cm.
Em metros, a distância da bola à barreira deve ser oficialmente igual a

