Uma professora querendo verificar o aprendizado de seus alunos, logo após a aula sobre triângulos, deu 18 palitos iguais para cada um, pedindo que formassem um único triângulo por vez, usando os 18 palitos sem parti-los. A quantidade de triângulos isósceles que é possível formarem é igual a
Ao olhar para o relógio, Marcos percebeu que eram X horas da manhã. Percebeu que se somasse a metade do tempo passado desde a última meia-noite com um quarto do tempo que falta para a próxima meia-noite obteria exatamente a hora atual. Que horas são?
Sabendo que o polinômio P(x ) = 3x2 + 32√3 x + 32k é um quadrado perfeito, pode-se dizer que a constante real k é um número
Dado um triângulo ΔABC e AB e BC medem, respectivamente, 5 cm e 17 cm. Quanto poderá medir o terceiro lado, sabendo-se que o valor do perímetro deste triângulo é um quadrado perfeito?
Um meteorologista em Teresina (PI) de posse de um pluviômetro cilíndrico de diâmetro 60 cm, colheu a água de um temporal, em seguida colocou em um recipiente também cilíndrico, cujo comprimento da circunferência da base mede 36 π cm. A altura que a água alcançou no pluviômetro, sabendo que no recipiente alcançou uma altura de 250 mm, foi de
Um árbitro de futebol possui três cartões no bolso: um todo amarelo, o outro todo vermelho e o terceiro com um dos lados amarelo e o outro vermelho. Se, num determinado jogo, o árbitro retira ao acaso um dos cartões e mostra, também ao acaso, uma das faces do cartão a um jogador, a probabilidade da face que o árbitro vê ser amarela e da outra face, mostrada ao jogador, ser vermelha é de aproximadamente.
Um jogo de futebol foi programado para ser realizado com
duração normal: 2 tempos de 45 minutos, com um intervalo de
15 minutos. O jogo começou pontualmente às 9:00 horas.
Um repórter cronometrou 6 jogadas que considerou as mais
importantes a partir do início do jogo e registrou suas marcas da
seguinte maneira:
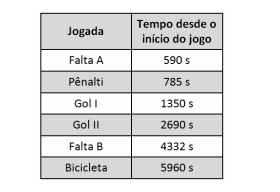
A partir das informações acima, assinale a afirmativa correta.
Um jogo de dados tem por objetivo obter as somas de 1 a 9,
sendo que o jogador pode escolher, em cada jogada, se vai lançar
um dado apenas ou os dois dados. Os participantes vão se
revezando no lançamento de dados e, quem conseguir todos
aqueles totais em primeiro lugar, e em qualquer ordem, será o
vencedor.
Sobre as chances de conseguir determinadas somas, é correto
afirmar que
Para ser aprovado em um concurso, o candidato precisaria acertar 3 de cada 5 questões de uma prova. Considerando que havia 45 questões na prova, quantas questões, no máximo, o candidato poderia errar para não ser reprovado e com quantos pontos, no mínimo, ele seria aprovado, se cada questão valesse um ponto?
Em uma empresa, os setores A e B fazem acordos diferentes relativos à carga horária semanal de trabalho. O setor A trabalha 38,5 horas por semana, enquanto o setor B trabalha 44,25 horas por semana. Quantas horas o setor B trabalha a mais por semana do que o setor A?
Em um colégio os alunos irão eleger o diretor, vice-diretor e tesoureiro entre os 20 professores do colégio. De quantas maneiras esta escolha pode ser feita?
O dono de um mercantil solicitou a compra
de alguns suprimentos para seu comércio, de
acordo com a tabela abaixo. Na entrega da
mercadoria, foi cobrado R$ 2,00 por cada 100kg
de produto transportado, adicionado de R$ 0,80
por cada quilômetro percorrido da distribuidora até
o mercantil, que dista da mesma, mil quilômetros.
Nessas condições, o valor total investido pelo
comerciante, com a compra da mercadoria,
acrescido do pagamento do respectivo frete, gira
em torno de:
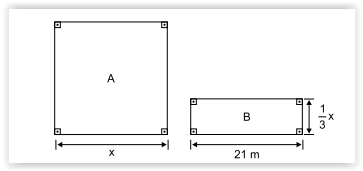
A medida do perímetro de um terreno quadrado A, de
lado x metros, é 1,5 vez maior que a medida do perímetro
de um terreno retangular B, de lados iguais a 21 e 1/3 x metros, conforme mostrado nas figuras.
O perímetro do terreno retangular B é, em metros, igual a
Com relação ao termo desconhecido de cada PA assinale a alternativa INCORRETA
O conjunto 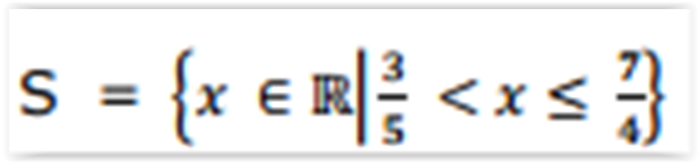
de qual inequação abaixo?