Oito professoras de uma escola de ensino infantil estavam cotando preços de barras de chocolates e de plásticos de embrulho para a produção dos ovinhos de páscoa que serão entregues a seus alunos. Dividirão, igualmente, todas as despesas. Elas compraram barras de chocolates que custava R$ 32,00 o quilo, e todas as embalagens saíram a R$ 72,00. No colégio, havia 200 alunos. Sabendo que cada ovinho produzido tem, exatamente, 125 gramas, e supondo que não houve desperdício do chocolate, o valor a ser pago por cada professora será de
Em uma receita de quibe de forno, além de alho, cebola, hortelã, sal e pimenta, são utilizados 500 gramas de carne moída, 250 gramas de trigo para quibe e 350 mililitros de água fervente. Essa receita serve 6 pessoas. Para um jantar de família com 18 pessoas que comerão quibe de forno, serão utilizados
Em um terminal de ônibus, há duas empresas que prestam serviço de transporte. Os ônibus da empresa A partem a cada 30 minutos. Já os ônibus da empresa B partem a cada 40 minutos. Às 20:30, os ônibus das duas empresas saem juntos. O próximo horário que os ônibus das duas empresas sairão juntos novamente é
Um médico atende pacientes em seu consultório das 8:00 às 18:00, interrompendo os atendimentos das 12:00 às 14:00 para almoço e descanso. Na agenda dele, a recepcionista verificou que são designados 20 minutos por paciente. Com base nesses dados, assinale a alternativa que apresenta o número máximo de pacientes que esse médico consegue atender por dia, sem trabalhar mais horas do que a estipulada.
Na entrada de uma casa de shows, foram instaladas 16 catracas para controle de acesso dos frequentadores. Os organizadores calculam que em cada catraca passam 6 pessoas por minuto. Considerando que não tem nenhum contratempo na entrada da casa de shows e que em nenhum momento essa quantidade de pessoas aumenta ou diminui, para entrar 8.640 pessoas nessa casa de shows, demora
Um encanador dispõe de três pedaços de barras de cano medindo 120 cm, 280 cm e 320 cm. Ele gostaria de dividir essas barras em pedaços iguais, com o maior comprimento possível. Nessas condições, quantos pedaços de cano ele poderia obter?
Uma loja vende, por dia, 1.000 m2 de piso a R$ 20,00 o m2. Seu proprietário percebeu que a cada R$ 1,00 de desconto dado no preço do m2 de piso, a loja vendia 50 m2 a mais, por dia. Por exemplo, no dia em que vendeu o piso a R$ 18,00, a loja vendeu 1.100 m2, e assim sucessivamente. Considerando x a quantidade de m2 de piso vendido em um dia e F o faturamento obtido com essa venda, a função que expressa F, em termos de x, é:
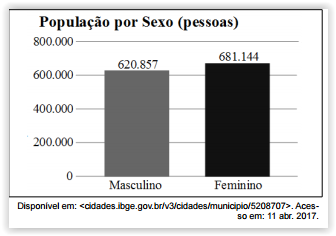
O gráfico a seguir mostra a população por sexo na cidade
de Goiânia, no ano de 2010
Segundo informações do IBGE, a população estimada da
cidade de Goiânia em 2016 era de 1.448.639 pessoas. De
acordo com essa informação e os dados apresentados no
gráfico, se a quantidade de pessoas do sexo feminino tivesse
em 2016 a mesma proporção apresentada em 2010
em relação ao total de pessoas da população de Goiânia,
a quantidade de pessoas do sexo feminino em Goiânia,
em 2016, seria, aproximadamente, de:
Dois amigos dispunham juntos de R$ 70,00 e foram a um
bar. Neste bar, eles comeram um prato de “tira-gosto”, no
valor de R$ 27,00, tomaram cinco cervejas e dois caldos.
Ao pagarem a conta, receberam R$ 3,80 de troco. Sabendo
que o preço de um caldo e de uma cerveja são iguais,
o preço da cerveja cobrado pelo bar foi de:
As aulas iniciaram e Ana Maria precisava
comprar os materiais escolares para sua
filha Carolina) Veja o que ela comprou.
Quanto será que ela gastou?
Considere um círculo de raio . Se o raio desse círculo for aumentado em 20%, o seu perímetro e sua área aumentarão respectivamente:
Em uma escola são ofertadas três opções de línguas estrangeiras, Inglês, Espanhol e Francês.
Matricularam-se 380 alunos e cada estudante poderá escolher uma e somente uma das três opções
ofertadas. O resultado das escolhas deverá ser mostrado em três setores circulares de um mesmo
gráfico. Sabendo-se que 76 alunos optaram pelo idioma Francês, então o ângulo central
correspondente a este idioma é:
Analisar os itens abaixo:
I - Para os conjuntos A = {1, 2, 3, 4} e B = {3, 4, 5, 6}, a intersecção dos conjuntos pode ser representada por A ∩ B = {3, 4}.
II - Para os conjuntos A = {j, k, l, m} e B = {m, o, p, q}, a união dos conjuntos pode ser representada por A ∪ B = {j, k, l, m, o, p, q}.
III - Para os conjuntos A = {20, 40, 60, 80} e B = {40, 60, 80, 100, 120}, a união dos conjuntos pode ser representada por A ∩ B = {40, 60, 80}, e a intersecção dos conjuntos pode ser representada por A ∪ B = {20, 40, 60, 80, 100, 120}.
IV - Para os conjuntos A = {f, g, h} e B = {v, x, w}, a intersecção pode ser representada por A ∩ B = {f, g, h, v, x, w}.
Está(ão) CORRETO(S):
Considerando-se as unidades de medida de capacidade, área e volume, marcar C para as afirmativas Certas, E para as Erradas e, após, assinalar a alternativa que apresenta a sequência CORRETA: (---) Para determinada dose de certa vacina, é necessário tomar 15mL de medicação, que deverá ocupar um volume equivalente a 15cm³. (---) Fernando tem dois terrenos, sendo um deles de área de 1.800.000cm² e o outro de 0,00023km². Ao se somar as áreas dos dois terrenos, a área total será igual a 410m². (---) Em certa solução, para cada litro de água, é necessário colocar 50mL de água sanitária. Se for utilizado um litro de água sanitária, serão necessários 200L de água.
Considerando-se que A = 68, B = 75, C = 80 e D = 82, analisar os itens abaixo: I - A razão entre A e D é igual a 34/41. II - A razão entre B e A é igual a 15/17. III - A razão entre C e D é igual a 40/41. IV - A razão entre B e C é igual a 15/16. Estão CORRETOS: