Quais das situações abaixo melhor se adequa para aplicação dentro do contexto da etnomatemática:
Sabe-se que P = (p e
| p é divisor de 180),
Q = (q e
| q < 30) e k é o número de elementos
do conjunto P — Q. Dessa forma, k vale:
A febre amarela é uma doença infecciosa aguda, de curta duração (no máximo 10 dias), gravidade variável, causada pelo vírus da febre amarela, que ocorre na América do Sul e na África. A única forma de evitar a febre amarela silvestre é a vacinação contra a doença. A vacina é gratuita e está disponível nos postos de saúde em qualquer época do ano.
Disponível em: Acesso em 22 mar. 2017
Um posto de saúde iniciou a vacinação contra a febre amarela com um lote de x doses. Sabe-se que o planejado é que o número de doses produzidas dobre a cada ano. Dessa maneira, após quanto tempo esse número passará a ser igual a 20 vezes o inicial?
(Use: log 2 = 0,3)
Joana foi ao supermercado e comprou 750 gramas de tomates, 1,5 quilos de batatas e 650 gramas de cebola. Ao todo sua mercadoria pesa:
Se considerarmos os nomes RAFAELA e MATHEUS como sendo um conjunto de letras cada um dos nomes. A intersecção entre estes conjuntos resulta no conjunto formado pelas letras:
Em uma P.G (progressão geométrica), o primeiro é igual a 5 e a razão é q= 2, determine seu último termo e indique a alternativa correta.
A área de um retângulo é igual a 120 cm². Sabendo
que a medida da base e a da altura desse retângulo
são números pares e consecutivos, então a medida do
perímetro do retângulo é:
Dada a matriz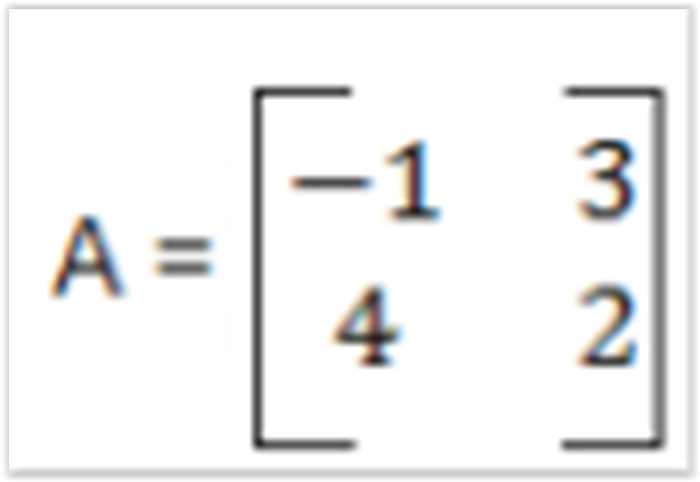 
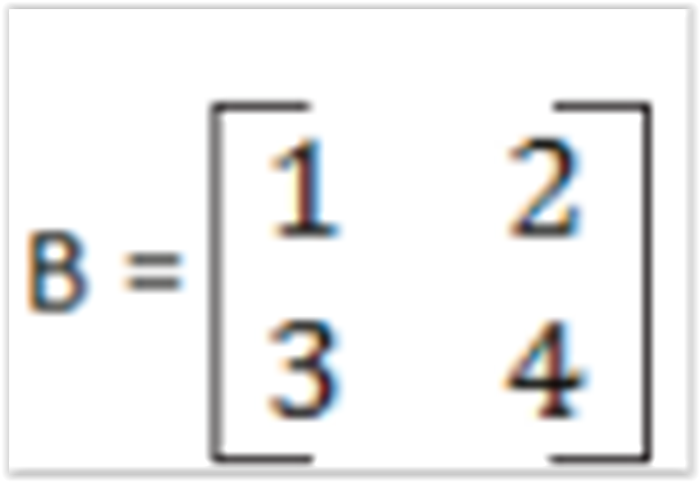
e a matriz 
, assinale a alternativa que apresenta a matriz C que
representa o produto da matriz A e B, ou seja, C = A * B.
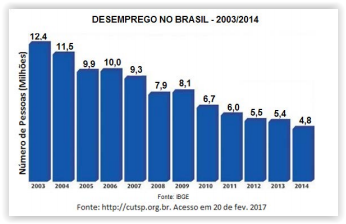
Observe o gráfico que mostra o número de desempregados no Brasil no período de 2003 a 2014.
A partir dos dados apresentados no gráfico, é possível afirmar que:
Gabriela usou 3/4 de duas dúzias de ovos para fazer quindim. Quantos ovos Gabriela usou para fazer os quindins?
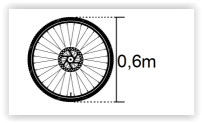
Considerando-se que a medida na imagem abaixo
representa o diâmetro da roda de uma moto, no mínimo,
quantas voltas completas essa roda deverá dar para
percorrer 0,1884km?
(Usar π = 3,14 )
Considerando-se as unidades de medida, assinalar a alternativa INCORRETA:
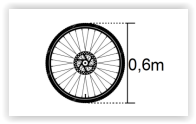
Considerando-se que a medida na imagem abaixo
representa o diâmetro da roda de uma moto, no mínimo,
quantas voltas completas essa roda deverá dar para
percorrer 0,1884km?
(Usar π = 3,14 )
Um aluno dispunha de 4 horas para fazer um simulado e ele fez da seguinte maneira: Em 1/4 do tempo, ele fez a parte de matemática; em 1/5 do tempo que sobrou, ele fez a prova de português; e as outras disciplinas ele fez no restante do tempo. O tempo dedicado às outras disciplinas, supondo que ele utilizou todo o tempo disponível, foi de
Um determinada fazenda produz bananas. Produziu, em Abril de 2017, 852.000 bananas, que foram distribuídas em caixas com capacidade para 300 bananas cada. Sabendo que, em média, 1/2000acabam estragando e não são colocadas nas caixas, a quantidade de caixas necessárias para comportar a produção que não estragou foi de, aproximadamente,
