Num conjunto há 5 elementos positivos e 5 elementos negativos. Escolhem-se 5 números desse conjunto e se efetua a multiplicação desses 5 números escolhidos. Em quantos casos tal multiplicação terá resultado negativo?
Em um curso de biblioteconomia, a razão entre o número de estudantes do sexo masculino e o número de estudantes do sexo feminino é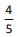 
e x corresponde ao número total de estudantes desse curso.
Com base nessa situação hipotética, assinale a alternativa que apresenta o valor de x.
Em um certo país da América do Sul, o combustível comercializado nos postos é uma mistura de uma parte de etanol com duas partes de gasolina. Considerando‐se esse combustível e um outro que apresenta uma mistura de três partes de etanol com cinco partes de gasolina e juntando‐se volumes iguais desses dois combustíveis, a nova relação de etanol para gasolina, nessa ordem, será igual a
Uma sequência numérica tem seu termo geral representado por an, para n ≥ 1. Sabe-se que a1 = 0 e que a sequência cujo termo geral é bn = an+1 - an, n ≥ 1, é uma progressão aritmética cujo primeiro termo é b1 = 9 e cuja razão é igual a 4.
O termo a1000 é igual a
O número de Euler, nome dado em homenagem ao matemático suíço Leonhard Euler, é um número irracional denotado por e, cuja representação decimal tem seus 4 primeiros algarismos dados por 2,718. Esse número é a base dos logaritmos naturais, cuja função f(x) = lnx = logex tem inúmeras aplicações científicas.
A respeito desse assunto, julgue o item a seguir.
A equação ln x = !4 tem uma única solução.
Cada j = 0, 1, …, 11 representa um mês do ano de 2017, isto é, j = 0 = janeiro, j = 1 = fevereiro, e assim sucessivamente. Se o mês j tem d dias, então j + 1/d representa o dia 1.º do mês j; j + 2/d representa o dia 2 do mês j, e assim sucessivamente, j + d/d = j + 1 representa o dia d do mês j. Dessa forma, cada dia do ano de 2017 pode ser representado por um número x do intervalo [0, 12]. Considere que, nessa representação, em cada dia x do ano de 2017, a porcentagem de água acumulada em relação à capacidade máxima do reservatório de determinada represa seja expressa pelo valor da função f(x) = x2 - 10x + 60.
A partir dessas informações, julgue o item que se segue.
Em 2017, a menor quantidade de água acumulada no reservatório foi inferior a 10% de sua capacidade máxima e foi atingida no dia 31/5/2017.
A figura seguinte mostra, em um sistema de coordenadas cartesianas ortogonais xOy, em que a unidade de medida é o metro, uma região retangular OABC. O lado OA mede 600 m e o lado OC mede 800 m.
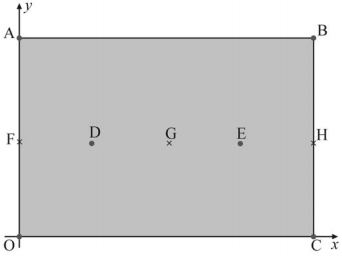
A figura mostra também os pontos F = ponto médio de OA, H = ponto médio de CB, G = centro do retângulo OABC, D = ponto médio de FG, e E = ponto médio de GH. Nos pontos O, A, B, C, D e E foram instalados pontos de acesso à Internet — wi-fi. Nessa configuração, o usuário consegue se conectar à Internet desde que o seu smartphone esteja a 200 m ou menos de qualquer desses pontos de acesso.
Com base nessas informações e na figura apresentada, julgue o próximo item.
Se um usuário tiver o seu smartphone no ponto R = (400, 100), então a conexão à Internet a partir de qualquer dos referidos pontos de acesso será impossível.
A figura seguinte mostra, em um sistema de coordenadas cartesianas ortogonais xOy, em que a unidade de medida é o metro, uma região retangular OABC. O lado OA mede 600 m e o lado OC mede 800 m.
A figura mostra também os pontos F = ponto médio de OA, H = ponto médio de CB, G = centro do retângulo OABC, D = ponto médio de FG, e E = ponto médio de GH. Nos pontos O, A, B, C, D e E foram instalados pontos de acesso à Internet — wi-fi. Nessa configuração, o usuário consegue se conectar à Internet desde que o seu smartphone esteja a 200 m ou menos de qualquer desses pontos de acesso.
Com base nessas informações e na figura apresentada, julgue o próximo item.
A tangente do ângulo COD é igual a 1,5.
Com relação a uma sequência numérica α1, α2, …, αn, julgue o item subsequente.
Considere que a sequência seja formada pelos seguintes termos, nessa ordem: 10, 12, 15, 19, 24, 30, 37. Nesse caso, a sequência numérica bj = αj + 1 - αj, em que j = 1, 2, …, 6 forma uma progressão aritmética.
A respeito dos números complexos, julgue o item a seguir.
As raízes cúbicas do número complexo z = 1 + i são os números complexos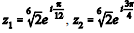 
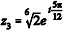
, e 
.
Julgue o item que se segue, relativo a matrizes e sistemas lineares.
Se
a é um número real e se o determinante da matriz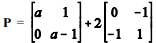 
for igual a zero, então a = -2 ou a = 1.
Acerca de probabilidade e estatística, julgue o próximo item.
Considere que fichas numeradas de 11 a 99 sejam colocadas em uma urna e que uma delas seja retirada aleatoriamente. Nesse caso, a probabilidade de o número da ficha retirada ter o algarismo das dezenas menor que o algarismo das unidades é inferior a 35%.
A respeito de história da matemática, julgue o item subsequente.
Em um dos paradoxos do filósofo Zenão é contada a história do herói Aquiles, que disputa uma corrida com uma tartaruga. Nessa corrida ambos desenvolvem velocidades constantes, mas a razão entre a velocidade da tartaruga e a de Aquiles é da forma 1/m, em que m > 1. Aquiles, por ser mais rápido, permite que a tartaruga largue na sua frente e, depois de ela ter percorrido d1 metros, ele inicia a sua corrida. Depois de certo tempo, o herói percorreu essa distância de d1 metros; a tartaruga havia percorrido mais d2 metros. Na etapa seguinte, repete-se o processo e Aquiles percorre essa distância de d2 metros, enquanto a tartaruga percorre mais d3 metros. Considerando que esse processo continue, Aquiles será capaz de ultrapassar a tartaruga depois de percorrer uma distância igual a d1 × m/[m - 1].
Numa academia de 530 alunos, 355 fazem musculação, 120 fazem aeróbico e 75 fazem as duas atividades físicas. Quantos alunos fazem musculação ou aeróbico?
Assinale a alternativa que corresponde ao resultado da divisão 1252:250.
