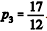A figura seguinte mostra, em um sistema de coordenadas cartesianas ortogonais xOy, em que a unidade de medida é o metro, uma região retangular OABC. O lado OA mede 600 m e o lado OC mede 800 m.
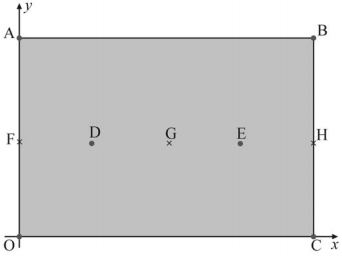
A figura mostra também os pontos F = ponto médio de OA, H = ponto médio de CB, G = centro do retângulo OABC, D = ponto médio de FG, e E = ponto médio de GH. Nos pontos O, A, B, C, D e E foram instalados pontos de acesso à Internet — wi-fi. Nessa configuração, o usuário consegue se conectar à Internet desde que o seu smartphone esteja a 200 m ou menos de qualquer desses pontos de acesso.
Com base nessas informações e na figura apresentada, julgue o próximo item.
A reta que contém os pontos B e E intercepta o eixo Ox no ponto de abscissa x = 300.
A figura seguinte mostra, em um sistema de coordenadas cartesianas ortogonais xOy, em que a unidade de medida é o metro, uma região retangular OABC. O lado OA mede 600 m e o lado OC mede 800 m.
A figura mostra também os pontos F = ponto médio de OA, H = ponto médio de CB, G = centro do retângulo OABC, D = ponto médio de FG, e E = ponto médio de GH. Nos pontos O, A, B, C, D e E foram instalados pontos de acesso à Internet — wi-fi. Nessa configuração, o usuário consegue se conectar à Internet desde que o seu smartphone esteja a 200 m ou menos de qualquer desses pontos de acesso.
Com base nessas informações e na figura apresentada, julgue o próximo item.
Considere que uma pessoa esteja em ponto P da região retangular de modo que o ângulo OPA seja igual a 90°. Nesse caso, se o cosseno do ângulo AOP for igual a 0,3, essa pessoa estará a mais de 200 m da origem O.
A respeito dos números complexos, julgue o item a seguir.
Se n for um número par e se p for um número real diferente de zero, então o polinômio zn + p = 0 tem, necessariamente, duas raízes reais distintas.
A respeito dos números complexos, julgue o item a seguir.
Se n > 1 for um número inteiro e se ω ≠ 1 for uma raiz n-ésima da unidade (isto é, ωn = 1), então 1 + ω +...+ ωn-1 = 0.
Julgue o item que se segue, relativo a matrizes e sistemas lineares.
Se 0 é a matriz nula n × n, se I é a matriz identidade n × n, e se P é uma matriz n × n tal que P2 + 2P + I = 0, então P é inversível.
Acerca de probabilidade e estatística, julgue o próximo item.
Situação hipotética: Na revisão de um livro, o editor contou 20 páginas que tiveram 0, 1, 2, 3 ou 4 erros; 36 páginas que tiveram 5, 6, 7, 8 ou 9 erros. Prosseguindo, ele obteve os valores mostrados na tabela a seguir.
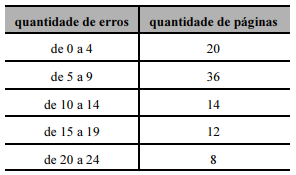
Assertiva: Nesse caso, a frequência relativa para os dados da classe modal da tabela é de 40%.
A respeito de história da matemática, julgue o item subsequente.
Os babilônicos possuíam um método próprio para o cálculo da raiz quadrada de um número, utilizando aproximações sucessivas. Para determinar o valor aproximado de
se estimava, primeiramente, um valor p1 para essa raiz e calculava-se o quociente 
. Com esses dois números calculava-se um novo valor p2, a média aritmética de p1 e q1, isto é, 
. Repetindo esse processo sucessivamente, obtinha-se uma aproximação da raiz quadrada. No método babilônico, se a estimativa inicial para 
for p1 = 1, então a terceira aproximação de será 
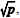
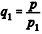
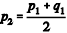
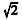
A respeito de operações com números e conjuntos, julgue o item.
Em uma pesquisa acerca da preferência em relação aos refrigerantes das marcas A e B, 200 pessoas foram ouvidas. 80 ouvintes disseram que gostam dos dois refrigerantes. São 15 os ouvintes que disseram não gostar de nenhum dos dois refrigerantes. Nesse caso, é possível que a quantidade de ouvintes que gostam apenas do refrigerante A seja igual à daqueles que gostam apenas do refrigerante B.
A prefeitura do Município de Fabriciano recebeu uma verba do Governo Federal que foi dividida entre três secretarias municipais: a de Cultura, Esportes e Saúde. A secretaria de Saúde recebeu três sétimos da importância, a de Esportes recebeu dois quintos e a de Cultura o resto.
Assinale a alternativa que apresenta CORRETAMENTE a fração da verba destina à secretaria de Cultura:
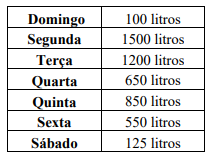
A caixa d'água de uma escola tem a forma de um cone circular reto, cujo raio é 1,25 metros e a altura 500 centímetros. Sabendo-se que o consumo de água da escola segue a tabela apresentada, determine em qual dia da semana a água irá acabar, considerando que o reservatório está cheio e começou a ser utilizado na segunda-feira (π = 3,14):
Um topógrafo tem em mãos um mapa de Coronel Fabriciano na escala de 1:5000. Com a ajuda de uma régua, mediu a distância no mapa entre dois bairros.
A distância encontrada, de 50,7cm, representa, na realidade:
João observa a sombra de um edifício projetada pelo sol sobre o piso plano com 2,5dam de comprimento. Conhecendo o Teorema de Tales, João utiliza um cabo de vassoura com 120cm de comprimento e mede a sua sombra que dá 0,8m.
Assinale a alternativa que apresenta a altura do edifício.
A figura abaixo representa duas circunferências concêntricas de centro A, cujos raios AB e AD medem, respectivamente, 9 e 2,5 cm. A área da coroa circular destacada abaixo, em cm2, é:
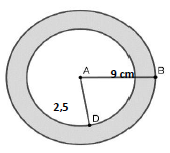
Em uma escola, a nota final do bimestre na disciplina de matemática é calculada pela média das notas obtidas em cada instrumento de avaliação oferecido, considerando seus pesos. Em uma determinada ocasião, o professor de matemática ofereceu três instrumentos de avaliação às suas turmas, conforme segue na tabela abaixo:
Supondo que um aluno tenha obtido as notas 7, 7 e 5 na pesquisa, lista de exercícios e prova, respectivamente, a nota final obtida no bimestre pelo aluno é:
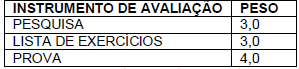
A medida do arco AB, em graus, é:
