Uma parede está sendo azulejada de tal forma que os azulejos de cada fileira formam uma sequência como a ilustrada a seguir
Sabendo que a fileira possui 40 azulejos, os dois últimos devem ser colocados em que posição?
Thiago foi a um pet shop para comprar um peixe Betta. A vendedora informou que o peixinho devia ficar em um aquário com paredes planas e sem tampa. Thiago se encantou com um aquário na forma de um prisma hexagonal, porém achou o preço muito caro e resolveu fazer o seu próprio aquário hexagonal. Conseguiu na vidraçaria a quantidade e os tamanhos exatos de recortes de vidro e usou alguns pedaços de fita para a construção de seu aquário. Para finalizar, prendeu um pedaço de alumínio de comprimento exato para o acabamento em cada encontro de duas peças de vidro. Para montar esse aquário, Thiago usou
Brincando com palitos, Luiza percebeu que, com 6 palitos, só era possível formar um retângulo, conforme a figura a seguir.
Se ela conseguir mais 8 palitos, quantos retângulos diferentes podem ser formados usando os palitos?
Uma escola realizou uma olimpíada do conhecimento entre os estudantes. O gráfico a seguir mostra a quantidade de medalhas que 5 alunos ganharam.
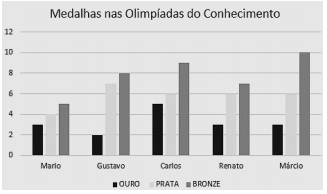
Qual aluno ganhou mais medalhas ao todo?
Um avião fez uma viagem de 3h e 30min com 285 passageiros. A companhia estimou que o custo operacional total dessa viagem foi de R$ 596.534,00.
Aproximadamente, qual o custo médio por hora viajada para cada passageiro?
O comprimento de um grande fio corresponde à soma dos comprimentos de 24 fios menores. São eles:
• 12 fios, cada um dos quais com comprimento que mede 14,7 cm;
• 4 fios, cada um dos quais com comprimento que mede 0,3765 km;
• 8 fios, cada um dos quais com comprimento que mede 13,125 dam.
Esse grande fio foi dividido em 3 fios de igual comprimento, chamados de unidade modelo.
Qual é a medida, em metros, do comprimento de uma unidade modelo?
No posto Alfa, o custo, para o consumidor, de um litro de gasolina é R$ 3,90, e o de um litro de etanol é R$ 2,70. Se o custo de um litro de uma mistura de quantidades determinadas desses dois combustíveis é igual a R$ 3,06, então o número de litros de gasolina necessários para compor 40 litros dessa mistura é igual a
Na sequência numérica 1, 2, 3, 6, 7, 8, 21, 22, 23, 66, 67, 68, ..., os termos se sucedem segundo um padrão. Mantido o padrão, o décimo quarto termo é o número
Sendo U = Q, a solução da inequação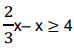 
é:
Considere as igualdades abaixo.
I. √0,25 = 0,5
II. 0,3 : 0,1 = 0,3 I
II. √50 = 5√2
São corretas as igualdades:
O valor de x que torna verdadeira a igualdade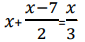 
é um número:
A velocidade de um veículo que trafegou por uma determinada via foi detectada como 95 Km/h por um sistema de radar. Considerando que a velocidade máxima permitida nessa via é de 70 Km/h, é correto afirmar que a velocidade do veículo excedeu a velocidade da via
Sendo 32 o primeiro termo de uma PG e 2 a sua razão, a diferença entre os termos a10 e a5 será:
Isabel tem 28 anos, seu irmão Pedro é 3 anos mais novo e sua outra irmã Raquel é 5 anos mais velha que Pedro. Calcule o Mínimo Múltiplo Comum (M.M.C.) da idade dos 3 irmãos.
Dos gráficos a seguir, qual o que melhor representa a função: f(x) = 2x + 4.
