As medidas de um triângulo isósceles ABC é AB=AC=5m e BC=8m. A razão entre sua altura e a sua área é:
Um pintor foi contratado para pintar as paredes laterais de um reservatório. Sabendo que esse reservatório tem forma de prisma hexagonal regular e sua área da base de 24√3m2 e sua altura 5m. Qual a área lateral total que deverá ser pintada?
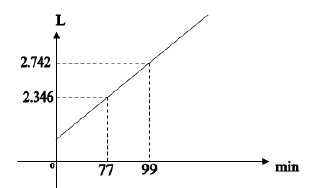
Em uma escola pública do município de São João do Araguaia há um reservatório/cisterna de água que possui 6000L (seis mil litros) de capacidade. Uma bomba d'água é ligada automaticamente quando a cisterna atinge certo nível de água e é desligada, também automaticamente, no instante em que ela completa sua capacidade. O gráfico abaixo representa o tempo que a bomba leva para encher completamente o reservatório desde o momento em que é ligada até o instante em que é desligada, automaticamente.
De acordo com o gráfico, em qual das alternativas abaixo está correta a função que representa o tempo que a bomba leva para encher completamente o reservatório?
Em uma pesquisa de opinião, para saber a rejeição dos eleitores em relação aos candidatos dos partidos A, B e C, foram obtidos os seguintes dados:
32% dos eleitores não votariam no candidato do partido A;
35% dos eleitores não votariam no candidato do partido B;
42% dos eleitores não votariam no candidato do partido C;
10% dos eleitores não votariam nos candidatos dos partidos A e B;
15% dos eleitores não votariam nos candidatos dos partidos A e C;
15% dos eleitores não votariam nos candidatos dos partidos B e C;
5% não votariam em nenhum dos três candidatos.
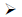
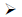
Considerando os dados obtidos nas pesquisas, o percentual de eleitores que votaria em qualquer um dos três candidatos é:
O salário de Arthur equivale a 3/7 do salário de Bárbara. Para que o salário de ambos fosse igual, o salário de Arthur teria que aumentar em 130% e, depois disso, ainda ser acrescido de R$ 60,00. Nas condições descritas, a soma dos atuais salários de Arthur e Bárbara, em reais, é igual a
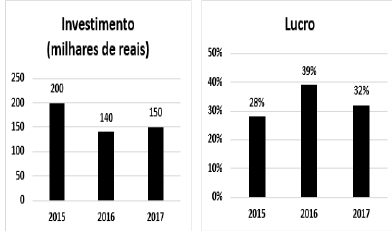
Os gráficos a seguir apresentam dados sobre o montante investido em debêntures de uma empresa e o lucro por ela obtido com esses títulos ao longo de três anos:
Com base na análise dos gráficos, a alternativa que apresenta de maneira CORRETA a diferença, em milhares de reais, do lucro entre o ano de 2016 e 2017 é:
A água contida no interior de um reservatório – que só tem água no seu interior – ocupa exatamente sete oitavos de sua capacidade. Se exatamente trezentos e cinquenta litros dessa água fossem consumidos antes de o reservatório ser reabastecido com qualquer quantidade de água, então o seu volume não ocupado equivaleria a 30% de sua capacidade total. Ao todo, quantos litros de água ainda cabem nesse reservatório?
Leia as afirmativas a seguir e marque a opção CORRETA:
A quinta parte de um número é igual ao dobro desse número menos 9 unidades. Esse número vale
Um estudante de matemática vai à padaria e diz ao balconista que gostaria de comprar 1,5 decímetro cúbico de leite. O balconista dominava as unidades de medida e, corretamente, trouxe ao cliente
Sabrina organizava sua caixa de brinquedos quando teve a ideia de dividir a caixa em 12 compartimentos. No primeiro, ela colocou 2 brinquedos. No segundo compartimento, ela colocou 4 brinquedos. No terceiro compartimento, 6 brinquedos. E permaneceu seguindo essa lógica até o décimo segundo compartimento. Sabendo-se que todos os brinquedos foram guardados exatamente nessa sequência, indique o número total de brinquedos de Sabrina.
Leia as afirmativas a seguir e marque a opção CORRETA:
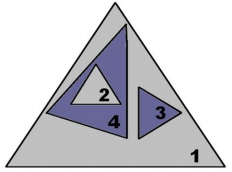
Se a figura, em que (2 ⊂ 4) ⊂ 1 e 3 ⊂ 1, representasse conjuntos numéricos, os triângulos 1, 2, 3 e 4 seriam, nessa ordem, os conjuntos
De todos os itens a seguir, o único incorreto é
Assinale dentre os itens a seguir aquele que representa um número múltiplo de 7.
