Resolva a equação a seguir e, ao final, assinale a alternativa que apresenta o resultado correto: x(x+4) + x(x+2) = 2x2 + 12
Marquinhos ganhou de seu pai R$ 120,00 (cento e vinte reais) de mesada. No dia seguinte, depositou 1/6 na poupança. Depois, usou 2/5 do restante para comprar figurinhas da Copa do Mundo e o restante ele gastou numa excursão escolar. Quanto, afinal, Marquinhos gastou nesta excursão?
Carlos aplicou a quantia de R$ 5.000,00 (cinco mil reais) e, após um ano, resgatou o montante de R$ 9.200,00 (nove mil e duzentos reais). Sabendo-se que o investimento se deu a juros simples, pode-se afirmar que a taxa mensal foi de:
Dois dados cúbicos, não viciados, com faces numeradas de 1 a 6, serão lançados simultaneamente. A probabilidade de que sejam sorteados dois números consecutivos, cuja soma seja um número primo, é de:
Joaquim chegou à padaria e pediu ao atendente 350g de muçarela, o que lhe custou R$ 11,20. Manuela, que comprou 600g do mesmo produto, deverá pagar, então:
Um levantamento foi realizado com 40 instituições financeiras, localizadas em uma região, com relação às taxas mensais de juros aplicadas para financiamento de veículos. Verificou-se que cinco instituições aplicam a taxa de 0,80% ao mês, duas aplicam a taxa de 1,20% ao mês, oito aplicam a taxa de 1,25% ao mês, x aplicam a taxa de 1,12% ao mês e y aplicam a taxa de 0,96% ao mês. Se a média aritmética destas taxas foi igual a 1,05%, então a soma da mediana e a moda correspondentes foi de
O lado de um triângulo equilátero mede 3 cm, unindo-se os pontos médios de seus lados obtém-se um novo triângulo equilátero. Unindo-se os pontos médios dos lados do novo triângulo obtém-se outro triangulo equilá-tero. Fazendo isso sucessivamente, determine a soma do perímetro de todos os triângulos que serão formados.
Se 
então log m é:
Em uma sala, estão 5 atletas de diferentes nacionalidades (Azerbaijão, Brasil, China, Dinamarca, Escócia). Em uma urna, estão as bandeiras dessas nacionalidades. Num sorteio simples, será selecionado um atleta da sala e após uma bandeira da urna. A probabilidade de o atleta sorteado não receba a bandeira de sua nacionalidade é de:
A figura a seguir exibe um mapa em que três ruas paralelas entre si são cortadas por outras três ruas, paralelas entre si e perpendiculares às três primeiras. As setas indicam os sentidos de circulação permitidos em cada rua.
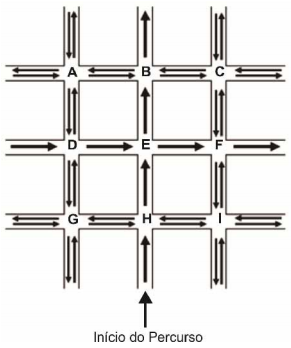
Os 9 cruzamentos entre essas vias foram nomeados por A, B, C, ... , I, como pode ser visto na figura. Um carro se encontra percorrendo a via destacada na figura, antes de entrar no cruzamento H. Ele deve seguir a sequência de instruções (após cada instrução, o carro percorre todo o quarteirão, até atingir o cruzamento e executar a instrução seguinte):
− 2ª rua à esquerda;
− 1ª rua à esquerda;
− 1ª rua à esquerda;
− 1ª rua à direita.
Sabendo que as instruções se referem sempre às ruas de conversão permitida (por exemplo, a instrução “1ª rua à esquerda" deve ser interpretada como “1ª rua à esquerda cuja conversão é permitida"), a pessoa atingirá, após seguir a última instrução e percorrer o quarteirão, o cruzamento
Dez funcionários possuem salários diferentes. Seus salários, em ordem crescente, são de R$ 2.000,00; R$ 2.100,00; R$ 2.200,00 e assim sucessivamente, sempre aumentando em R$ 100,00 em relação ao anterior. O número mínimo desses funcionários que devem ser sorteados ao acaso para que se tenha certeza de que os que não foram sorteados tenham soma dos salários inferior a R$ 14.000,00 é igual a
Sendo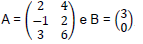 
, então o produto AxB é igual a:
Considerando as funções: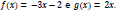 
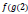
e . O valor numérico da expressão 
será:
Complete a lacuna abaixo: A __________ é simétrica (figura/gráfico que, ao dividi-la em partes iguais e sobrepô-las, as partes coincidem-se perfeitamente) em relação ao eixo horizontal, ou seja, à abscissa x.
A respeito dos conceitos e fundamentos da estatística, assinale a alternativa que apresenta a melhor definição sobre a média aritmética ponderada:
