Questões de Concurso – Aprova Concursos

Folha de respostas:

1
- a
- b
- c
- d
- e
2
- a
- b
- c
- d
- e
3
- a
- b
- c
- d
- e
4
- a
- b
- c
- d
- e
5
- a
- b
- c
- d
- e
6
- a
- b
- c
- d
- e
7
- a
- b
- c
- d
- e
8
- a
- b
- c
- d
- e
9
- a
- b
- c
- d
- e
10
- a
- b
- c
- d
- e
11
- a
- b
- c
- d
- e
12
- a
- b
- c
- d
- e
13
- a
- b
- c
- d
- e
14
- a
- b
- c
- d
- e
15
- a
- b
- c
- d
- e

2611)

Q807111 - VUNESP - 2019 - Prefeitura de Valinhos - SP - Agente Administrativo II,

A figura mostra as medidas internas, em centímetros, de
uma caixa na forma de um prisma reto de base retangular,
com 15 cm de altura

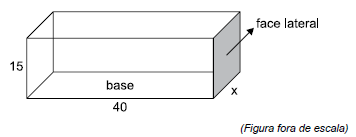
Sabendo que o volume dessa caixa é 21 000 cm3, então,
a área da face lateral, destacada na figura, é

a) 450 cm2.
b) 475 cm2.
c) 500 cm2.
d) 525 cm2.
e) 550 cm2.

2612)

Q807147 - VUNESP - 2019 - Prefeitura de Valinhos - SP - Assistente Social,

André e Daniel receberam uma mesma quantia em dinheiro.
Eles gastaram, desse dinheiro, a mesma quantia por dia durante
vários dias. Após 57 dias, André ficou com R$ 43,00,
e após 58 dias, Daniel ficou com R$ 29,00. O valor que cada
um desses rapazes recebeu foi

a) R$ 613,00.
b) R$ 783,00.
c) R$ 841,00
d) R$ 910,00.
e) R$ 1.002,00

2613)

Q807154 - VUNESP - 2019 - Prefeitura de Valinhos - SP - Assistente Social,

A média aritmética simples das idades de 32 pessoas
é 36 anos. Dez dessas pessoas têm 70 anos e dez têm
15 anos de idade. Considerando somente as demais pessoas,
se as mais novas têm 22 anos, a mais velha terá
uma idade, em anos, no máximo igual a

a) 40
b) 45
c) 50
d) 55
e) 60

2614)

Q803296 - CESPE - 2019 - CGE-CE - Auditor de Controle Interno - Área de Fomento ao Controle Social

Conforme o texto CB1A5-I, se, para cada j = 0, 1, 2, ..., M_j for o conjunto dos municípios cearenses que celebraram, pelo menos, j convênios com o governo estadual, então o conjunto dos municípios que não celebraram nenhum convênio com o governo do estado será representado pelo conjunto

a)
M₀.
b)
M₁ - M₀.
c)
M₁ ∩ M₀
d)
M₀ - M₁.
e)
M₀ ∪ M₁.

2615)

Q805920 - CEV-URCA - 2019 - Prefeitura de Brejo Santo - CE - Auditor Fiscal

Calcule a área de um triângulo ABC no qual $A B em moldura superior fecha moldura igual a 4 espaço c m vírgula espaço B C em moldura superior fecha moldura igual a 5 espaço c m espaço e espaço A B com conjunção lógica sobrescrito C igual a 60 º$

a) 5 cm²
b) 5 √3 cm ²
c) 10 √3 cm ²
d) 10 cm²
e) 20 cm²

2616)

Q805925 - CEV-URCA - 2019 - Prefeitura de Brejo Santo - CE - Auditor Fiscal

Um vendedor dá um desconto de 10% num determinado produto. Como o produto continuou sem muita saída, o vendedor deu outro desconto, desta feita, de 8%. Pergunta-se: Qual o desconto total dado pelo vendedor para esse produto?

a) 18%
b) 17,2%
c) 15%
d) 18,2%
e) 18,8%

2617)

Q781593 - IDECAN - 2019 - IF-PB - Professor EBTT - Informática - Perfil 03

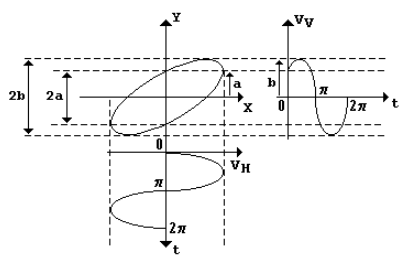
Qual o ângulo de defasagem entre dois sinais, que apresenta na tela do osciloscópio a imagem da Figura abaixo (conhecido como figuras de lissajous). Onde 2a = 5, 2b = 10.

a)
100°
b)
90°
c)
150°
d)
30°
e)
0°

2618)

Q781668 - IDECAN - 2019 - IF-PB - Professor EBTT - Matemática - Perfil 01

Davi é um menino de 15 anos de idade. Seus pais, muito preocupados com o futuro financeiro dele decidem aplicar uma quantia de R$ 20.000,00 para que ele possa retirar quando completar 18 anos. Sabendo que a rentabilidade anual é de 6% qual será o montante, aproximadamente, retirado quando Davi completar seus 18 anos?

a) R$ 23.820,32.
b) R$ 23.600,00
c) R$ 23.001,52
d) R$ 22.810,31
e) R$ 21.540,12

2619)

Q781670 - IDECAN - 2019 - IF-PB - Professor EBTT - Matemática - Perfil 01

Determine o valor de x, de modo que 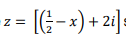seja um número imaginário puro.

a)
b)
1
c)
d)
2
e)

2620)

Q781675 - IDECAN - 2019 - IF-PB - Professor EBTT - Matemática - Perfil 01

Assinale a alternativa correta com relação a definição de uma parábola.

a)
Uma parábola pode ser escrita na forma y(x) = ax² + bx + c com a igual a zero.
b) Uma parábola é um conjunto de pontos com distâncias constantes para uma reta.
c) Uma parábola é uma curva cuja distância até o ponto focal é fixa, independente do ponto na curva.
d)
Uma parábola pode ser representada pela função y(x) = ax² + bx + c, sendo a pertencente aos reais.
e) O conjunto de todos os pontos de um plano equidistantes de um ponto fixo e de uma reta fica desse plano.

2621)

Q781682 - IDECAN - 2019 - IF-PB - Professor EBTT - Matemática - Perfil 01

A partir da tendência metodológica baseada na resolução de problemas, como se deve trabalhar situações problemas no campo da Matemática na sala de aula?

a) Utilizando situações do cotidiano.
b) Trabalhando de forma rotineira e mecânica as definições e demonstrações.
c) Enfatizando apenas a aplicação e sistematização dos conhecimentos.
d) Treinando excessivamente as definições, técnicas e demonstrações.
e) Trabalhando com testes objetivos e subjetivos para captar a totalidade do fenômeno.

2622)

Q781694 - IDECAN - 2019 - IF-PB - Professor EBTT - Matemática - Perfil 02

Uma empresa produz peças de madeira com tamanho fixo. A quantidade Q de cada peça de madeira, dada em metros, vendida é função do preço P em real por metro. Desta forma, podemos afirmar que a receita das vendas conseguida com o preço de venda P é igual a R(P) = Pf (P). Sabendo-se ainda que f(20) = 10.000,00 e f'(20) = -350,00, calcule o valor de R'(20).

a) R$ 1.000,00
b) R$ 3.000,00
c) R$ 7.000,00
d) R$ 13.000,00
e) R$ 17.000,00

2623)

Q781702 - IDECAN - 2019 - IF-PB - Professor EBTT - Matemática - Perfil 02

Considere que tenhamos uma equação diferencial na forma dada como M (x,y)dx + N (x,y)dy = 0. As funções podem ser escritas como M (x,y) = f(x)g(y) e N (x,y) = F(x)G(y). A equação M(x,y)dx + N(x,y)dy = 0 pode ser considerada

a)
uma equação de Riccati.
b)
uma equação diferencial separável.
c)
uma equação diferencial não-separável.
d)
uma equação de Bernoulli de ordem superior.
e)
uma equação diferencial de segunda ordem.

2624)

Q781707 - IDECAN - 2019 - IF-PB - Professor EBTT - Matemática - Perfil 02

Seja 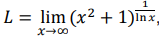então,

a)
L = 0.
b)
L = 1.
c)
L = e.
d)
L = e².
e)
L = ∞.

2625)

Q781719 - IDECAN - 2019 - IF-PB - Professor EBTT - Matemática - Perfil 02

Os valores de a e b para que os planos 5x + 2y + 4z + 3 = 0 e (a - 4)x + 8y + (b - 2)z + 5 = 0 sejam paralelos, são:

a)
a = 24 e b = 18.
b)
a = 8 e b = 3.
c)
a = -2 e b = -3.
d)
a = 3 e b = -2.
e)
a = 6 e b = -1.

Questões de Concurso – Aprova Concursos

Milhares de questões com o conteúdo atualizado para você praticar e chegar ao dia da prova preparado!