Observe a figura e responda:
Cada uma dessas partes representa que fração retângulo?
Um carpinteiro guarda, em quatro caixas opacas (não transparentes), dois tipos de parafusos que se diferenciam apenas por suas tonalidades (claros e escuros). Ele sabe exatamente quantos parafusos de cada tipo há em cada caixa. As quantidades estão apresentadas a seguir.
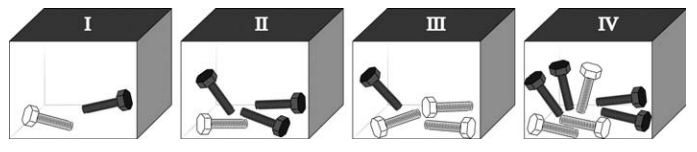
Considere que esse carpinteiro queira retirar, sem olhar, um parafuso de uma de suas caixas, esperando ter a maior probabilidade de obter um de cor clara.
A retirada deve ser feita da caixa
A obesidade é um dos maiores fatores de risco para doenças e, para evitá-la, é importante conhecer as categorias de peso, que podem ser identificadas através do Índice de Massa Corpórea (IMC). O IMC é a razão entre a massa de uma pessoa (em quilograma) e o quadrado de sua altura (em metro), ou seja,
. As categorias para os resultados do IMC são mostradas na tabela.
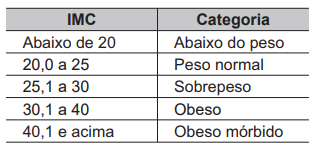
Considere uma pessoa com obesidade mórbida, com I MC igual a 42 e altura 1 ,50 m. Para evitar problemas de saúde, seu médico lhe recomendou que emagrecesse o suficiente para chegar na categoria de sobrepeso.
A quantidade mínima de massa, em quilograma, que essa pessoa deve perder para alcançar a meta proposta pelo médico é
Com a finalidade de motivar seus funcionários, uma empresa premia o funcionário do mês organizando um sorteio de brindes. O sorteio é feito colocando-se em um globo não transparente: 3 bolas vermelhas, 5 bolas azuis, 8 bolas amarelas e 4 bolas brancas. O funcionário do mês deve retirar uma bola ao acaso e seu prêmio será determinado de acordo com a cor da bola: a bola vermelha corresponde a um televisor; a bola azul, a uma bicicleta; a bola amarela, a um ventilador; e a bola branca, a um micro-ondas.
Qual é a probabilidade de o funcionário do mês ganhar um televisor?
O gerente de uma concessionária, com a finalidade de mostrar o bom desempenho de sua equipe, traçou um plano de ação para seus vendedores baseado no número de vendas de veículos do ano anterior. Ele apresentou a quantidade de veículos vendidos , distribuída mensalmente, conforme o gráfico.
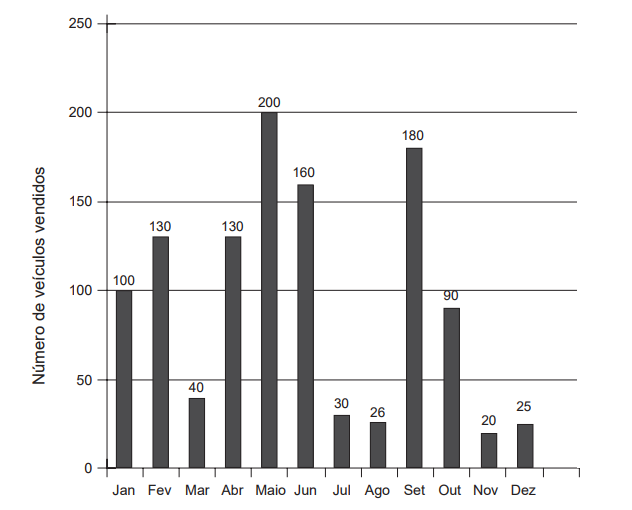
Seu plano para o próximo ano é estabelecer, como meta de vendas mensais, a média aritmética dos seis meses com maiores quantidades de veículos vendidos apresentados no gráfico.
Qual é o número mínimo de veículos que deverão ser vendidos para se cumprir a meta projetada pelo gerente?
O grupo para análise de inquéritos administrativos de uma corporação é formado por 3 tenentes e 5 sargentos. Quantas comissões de inquérito, constituídas por 5 pessoas, podem ser formadas, contendo, no mínimo, 1 tenente?
Seis livros diferentes estão distribuídos em uma estante de vidro, conforme a figura abaixo:
Considerando-se essa mesma forma de distribuição, de quantas maneiras distintas esses livros podem ser organizados na estante?
Sejam M = 
e N = 
, matrizes quadradas de ordem 3, e x ∈ R.
Se det (M) > det (N), então é correto afirmar que
Seja a equação geral da reta ax + by + c = 0. Quando a = 0, b ≠ 0 e c ≠ 0, a reta
A superfície lateral de um cone, ao ser planificada, gera um setor circular cujo raio mede 10 cm e cujo comprimento do arco mede 10π cm. O raio da base do cone, em cm, mede
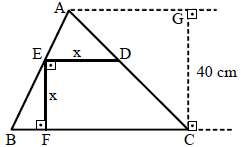
Na figura, se BC = 60 cm, a medida de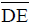 
, em cm é
A área de um triângulo retângulo cuja hipotenusa mede 
cm e um dos catetos mede 4 cm é igual a:
Uma enquete demonstrou que 17% das empresas devem algum tipo de imposto do ano anterior, e, desse grupo, são 13% que devem algum tipo de imposto dos últimos
dois anos. Em relação ao total de empresas da enquete, a porcentagem das empresas que devem apenas os impostos do ano anterior é de, aproximadamente,
Em determinado concurso público para o cargo de professor,
1.200 candidatos inscreveram-se para as áreas de física,
matemática e química. Sabe-se que, dos inscritos, 230 podem
lecionar matemática e física; 380 podem lecionar física e
química; 220 podem lecionar matemática e química; 560
podem lecionar matemática; e 120 podem lecionar as três
disciplinas. A partir dessas informações, é possível construir o
denominado diagrama de Euler-Venn, como mostra a figura
a seguir.
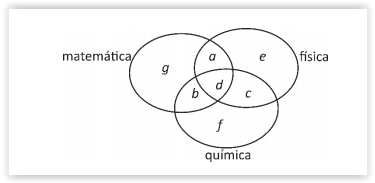
O diagrama mostra subconjuntos disjuntos e cada uma das
letras de a a g indica a quantidade de elementos do
respectivo subconjunto. Por exemplo, g é a quantidade de
inscritos que só lecionam matemática. Com base nessas
informações e no diagrama, julgue os itens seguintes.
Há mais inscritos que podem lecionar somente matemática e física que inscritos que podem lecionar as três disciplinas.
Na figura a seguir, as retas r1, r2, r3, r4 e r5 são paralelas; as
retas s1 e s2 são transversais; X, Y e Z e os números ao lado
dos segmentos das retas transversais indicam seus
respectivos comprimentos.
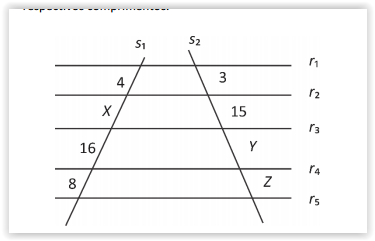
Com relação à figura, julgue os itens seguintes.
Y + Z = 24.
