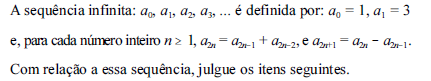Questões de Concurso – Aprova Concursos

Folha de respostas:

1
- a
- b
- c
- d
2
- a
- b
- c
- d
3
- a
- b
- c
- d
4
- a
- b
- c
- d
5
- a
- b
- c
- d
- e
6
- a
- b
- c
- d
- e
7
- a
- b
- c
- d
- e
8
- Certo
- Errado
9
- Certo
- Errado
10
- a
- b
- c
- d
11
- a
- b
- c
- d
- e
12
- a
- b
- c
- d
- e
13
- a
- b
- c
- d
- e
14
- a
- b
- c
- d
- e
15
- a
- b
- c
- d
- e

2356)

Q701545 - IBFC - 2018 - CBM-SE - Soldado do Corpo de Bombeiro

Um atleta corre numa pista circular cujo diâmetro é igual a 180 metros. Se no final da corrida esse atleta deu 12 voltas completas na pista então a distância total percorrida, em metros, foi:

a)
180π
b)
2160π
c)
5320π
d)
1080π

2357)

Q701906 - IBFC - 2018 - CBM-SE - Cadete do Corpo de Bombeiros

produto entre os números complexos Z₁ = 3√2(cos 45º + i.sen45º) e Z₂= 2 + i , é igual a:

a) 3+9i
b) 9+3i
c) 9-3i
d) -3+9i

2358)

Q701913 - IBFC - 2018 - CBM-SE - Cadete do Corpo de Bombeiros

A solução da inequação cos χ < 0,5 para 0 ≤ χ < 360° , é:

a)
(χ ∈ ℜ/ 30º < χ < 330º}
b)
(χ ∈ ℜ/ 90º < χ < 270º}
c)
(χ ∈ ℜ/ 60º < χ < 300º}
d)
(χ ∈ ℜ/ 150º < χ < 210º}

2359)

Q706324 - Adm&Tec - 2018 - Prefeitura de Tacaratu - PE - Recepcionista,

Leia as afirmativas a seguir:

I. Se um triângulo possui arestas com dimensões iguais a 34 hm, 30 hm e 27 hm, então seu perímetro será igual a 91 hm.

II. Se um triângulo possui arestas com dimensões iguais a 9 km, 13 km e 13 km, então seu perímetro será inferior a 27 km.

III. Se um triângulo possui arestas com dimensões iguais a 3 cm, 7 cm e 9 cm, então seu perímetro será igual a 21 cm.

Marque a alternativa CORRETA:

a) Nenhuma afirmativa está correta.
b) Apenas uma afirmativa está correta.
c) Apenas duas afirmativas estão corretas.
d) Todas as afirmativas estão corretas.

2360)

Q706792 - CONSCAM - 2018 - Prefeitura de Avaré - SP - Monitor

O total, em centímetros, da soma entre 25 metros e 128 decímetros é igual a:

a) 3.780.
b) 2.628.
c) 1.530.
d) 1.305.
e) 262,8.

2361)

Q706797 - CONSCAM - 2018 - Prefeitura de Avaré - SP - Monitor

Marcos aplicou R$ 387,00 à taxa de juros simples de 3% ao mês por 2 meses. O valor que será resgatado por Marcos ao final do período será:

a) R$ 401,22.
b) R$ 410,22.
c) R$ 412,32.
d) R$ 415,23.
e) R$ 422,23.

2362)

Q706879 - CONSCAM - 2018 - Prefeitura de Avaré - SP - PEB I (Professor de Educação Básica I),

Um reservatório com capacidade para 12 metros cúbicos de água está com 2000 litros de água. A razão da quantidade de água que está no reservatório para a capacidade total do reservatório é de:

a) 1/3.
b) 1/6.
c) 2/3.
d) 1/4.
e) 2/5.

2363)

Q703438 - CESPE - 2018 - ABIN - Oficial de Inteligência - Conhecimentos Gerais

A quantidade de maneiras distintas de se formar um time de vôlei com seis integrantes, sendo três homens da família Turing e três mulheres da família Gödel, é superior a 700.

Errado
Certo

2364)

Q703565 - CESPE - 2018 - ABIN - Oficial Técnico de Inteligência - Conhecimentos Gerais

Existem infinitos valores inteiros de p e q tais que a_p = a_q.

Errado
Certo

2365)

Q703882 - IBGP - 2018 - Prefeitura de Coronel Fabriciano - MG - Motorista de Veículos Pesados,

Sabe-se que as idades das três filhas de Pedro são iguais aos três primeiros números primos positivos. Com base nisso, é CORRETO afirmar que as idades das filhas de Pedro são, respectivamente:

a) 2, 3 e 5 anos.
b) 3, 5 e 6 anos.
c) 3, 6 e 7 anos
d) 5, 7 e 11 anos.

2366)

Q698228 - CONSCAM - 2018 - Prefeitura de Fernão - SP - Assistente Social,

O valor de x na da equação 3x – 3 = - 18 corresponde a:

a) 5.
b) -5.
c) 7.
d) -7.
e) 0.

2367)

Q698230 - CONSCAM - 2018 - Prefeitura de Fernão - SP - Psicólogo,

Sendo A = 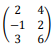e B = , então o produto AxB é igual a:

2368)

Q698463 - METROCAPITAL - 2018 - Prefeitura de Cerquilho - SP - Professor de Ensino Fundamental II - Arte,

Durante um curso de Matemática voltado a concursos públicos, Pedro faltou 8% do total de 75 aulas. Dessa forma, pode-se afirmar que Pedro não esteve presente em:

a)
4 aulas.
b) 5 aulas.
c) 6 aulas.
d) 7 aulas.
e) 8 aulas.

2369)

Q698622 - METROCAPITAL - 2018 - Prefeitura de Cerquilho - SP - Professor de Ensino Fundamental II - Matemática

Que número deve ser somado ao numerador e ao denominador da fração 2/3 (dois terços) para que ela tenha um aumento de 25% (vinte e cinco por cento):

a) 1 (um).
b) 3/4 (três quartos).
c) 3 (três).
d) 5 (cinco).
e) 2/4 (dois quartos).

2370)

Q698627 - METROCAPITAL - 2018 - Prefeitura de Cerquilho - SP - Professor de Ensino Fundamental II - Matemática

A área de um quadrado mais o seu perímetro é igual a 21. Qual é a medida do lado deste quadrado?

a) -7 unidades de medida.
b) 3 unidades de medida.
c) 7 unidades de medida.
d) 5 unidades de medida.
e) 9 unidades de medida.

Questões de Concurso – Aprova Concursos

Milhares de questões com o conteúdo atualizado para você praticar e chegar ao dia da prova preparado!