Para utilizar o autoatendimento de certo banco, o cliente deve utilizar uma senha silábica composta de três sílabas distintas. Para que possa acessar a sua conta em um caixa eletrônico, o cliente deve informar a sua senha silábica da seguinte maneira:
• primeiramente, é apresentada uma tela com 6 conjuntos de 4 sílabas distintas cada um, dos quais apenas um contém a primeira sílaba da senha do cliente, que deve, então selecionar esse conjunto;
• em seguida, é apresentada uma segunda tela com 6 novos conjuntos de 4 sílabas distintas cada um, dos quais apenas um contém a segunda sílaba da senha do cliente, que deve, então, selecionar esse conjunto;
• finalmente, é apresentada uma terceira tela com 6 novos conjuntos de 4 sílabas distintas cada um, dos quais apenas um contém a terceira sílaba da senha do cliente, que deve, então, selecionar esse conjunto.
A informação da senha silábica só será considerada correta se cada uma das 3 sílabas que compõem essa senha for informada na ordem solicitada: a primeira sílaba deverá estar no conjunto selecionado na primeira tela; a segunda sílaba, no conjunto selecionado na segunda tela; e a terceira sílaba, no conjunto selecionado na terceira tela.
Com base nessas informações, julgue os próximos itens.
Se um indivíduo conseguir visualizar e anotar os 3 conjuntos de 4 sílabas selecionados corretamente por um cliente em um terminal de autoatendimento e, em seguida, listar todas as possibilidades para a senha silábica desse cliente, para, então, escolher uma dessas possíveis senhas, a probabilidade de que essa escolha coincida com a senha do correntista será inferior a 0,01.
Sete bolas brancas e sete bolas pretas foram distribuídas em quatro caixas, e a figura abaixo mostra quantas bolas cada caixa contém.
Sabe-se que:
- cada caixa contém, pelo menos uma bola branca;
- a terceira caixa contém quantidades iguais de bolas brancas e pretas;
- a quarta caixa possui mais bolas brancas do que pretas.
Retirando ao acaso uma bola de cada caixa, a probabilidade de que todas sejam brancas é:
Em uma sala estão 60 candidatos de um concurso público, aguardando a distribuição do caderno de questões da prova. Dos 60 candidatos, 24 usam óculos, 33 usam óculos ou são canhotos e, 48 são destros. Um candidato será escolhido ao acaso para verificar que o pacote contendo as provas está lacrado. Considerando que nenhum dos 60 candidatos é ambidestro, determine a probabilidade de ser escolhido um candidato que use óculos e seja canhoto.
Um candidato a um programa de pós-graduação precisa passar por dois tipos de prova: oral e escrita. Os resultados das provas são independentes, e as probabilidades de aprovação são de 1/4 na prova oral, e 3/4, na prova escrita.
A aceitação do aluno está vinculada à aprovação em duas provas consecutivas em uma série de três aplicadas na ordem: oral, escrita, oral.
Qual é a probabilidade de aprovação do candidato?
O seguro de um determinado modelo de veículo é R$ 1.200,00 (mil e duzentos reais) e a seguradora paga ao segurado R$ 25.000,00 (vinte e cinco mil reais) em caso de sinistro. Sabendo-se que o lucro médio da seguradora por veículo segurado desse modelo é de R$ 200,00 (duzentos reais), qual a probabilidade de ocorrer sinistro?
Maria tem dez anos de idade e já se decidiu: quer ser ou advogada ou bióloga ou veterinária, quer estudar ou na UFMG ou na USP ou na UFRJ, e, depois de formada, quer trabalhar ou em Brasília ou em Florianópolis ou em Porto Alegre. Com base nessa situação hipotética e considerando que os eventos sejam independentes e tenham a mesma probabilidade, a probabilidade de Maria vir a ser advogada, formar-se na USP e trabalhar em Brasília será
O desenho esquemático (Box-Plot) abaixo representa a distribuição do tempo em anos de contribuição à previdência de aposentados de uma empresa até uma certa data.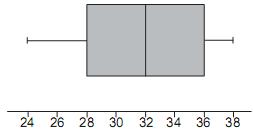
Se forem selecionados dois aposentados aleatoriamente, a probabilidade de que pelo menos um deles se tenha aposentado entre 28 e 32 anos é
Três urnas contêm 9 bolas numeradas de 1 a 9, cada. Um experimento consiste em selecionar uma bola de cada urna e verificar o número de resultados coincidentes.
A probabilidade de que haja exatamente dois números coincidentes dentre os três números selecionados é
O Ministério da Fazenda pretende selecionar ao acaso 3 analistas para executar um trabalho na área de tributos. Esses 3 analistas serão selecionados de um grupo composto por 6 homens e 4 mulheres. A probabilidade de os 3 analistas serem do mesmo sexo é igual a
Em uma estante estão posicionados 10 bonecos de plástico, todos do mesmo modelo, sendo 4 verdes, 4 azuis e 2 amarelos. João pegará 2 bonecos, um após o outro, sem devolvê-los à estante. Determine a probabilidade de João pegar dois bonecos azuis.
O Sr. Ramoile, professor de Estatística aposentado, vem há muito tempo acompanhando os dados sobre custos e faturamento do restaurante de sua filha Cecília. O restaurante funciona todos os dias da semana e o Sr. Ramoile concluiu que: o custo diário do restaurante segue uma distribuição normal, com média igual a R$ 500,00 e desvio- padrão igual a R$ 10,00 e que o faturamento diário, também, apresenta uma distribuição normal, com média R$ 800 e desvio-padrão R$ 20. Como o Sr. Ramoile conhece muito bem os princípios básicos da estatística, ele sabe que, se uma variável Z seguir uma distribuição normal padrão, então Z tem média 0 e variância 1. Ele também sabe que a probabilidade dessa variável Z assumir valores no intervalo entre 0 < Z < 2 - ou seja, entre a média 0 e 2 desvios-padrão - é, aproximadamente, igual a 0,4772. Cecília, muito preocupada com o futuro de seu restaurante, perguntou a seu pai se ele poderia verificar a probabilidade de, em um dia qualquer, o custo ser maior do que R$ 520,00 e o faturamente ficar no intervalo entre R$ 760,00 e R$ 840,00. Após alguns minutos, o Sr. Ramoile disse, acertadamente, que as respectivas probabilidades são, em termos percentuais, iguais a
Em um órgão público, 40 relatórios de prestação de contas
que apresentaram erro serão novamente analisados e, para que esse
trabalho seja executado mais eficientemente, esses relatórios foram
separados em dois grupos (A e B), cada um com 20 relatórios. Em
cada grupo, os relatórios foram classificados, de acordo com o erro
apresentado, em EM = relatório com erro de natureza média;
EG = relatório com erro de natureza grave; ou EGS = relatório com
erro de natureza gravíssima. Escolhendo-se, aleatoriamente, um
relatório do grupo A, sabe-se que as probabilidades de ele ser
classificado como EM, EG ou EGS são, respectivamente:
PA(EM) = 0,5; PA(EG) = 0,3; PA(EGS) = 0,2. No caso de relatório
do grupo B, as probabilidades são: PB(EM) = 0,1; PB(EG) = 0,6;
PB(EGS) = 0,3.
A probabilidade de se escolher, aleatoriamente, três relatórios,
sendo dois do grupo A e um do grupo B, todos classificados
como EGS, é expressa por (4/20) × (3/19) × (6/20).
Atenção: Para resolver às questões de números 52 e 53, considere os dados abaixo:
A empresa de aviação T tem 4 balcões de atendimento ao público: A, B, C e D. Sabe-se que, num determinado dia, os balcões A e B atenderam, cada um, a 20%; C e D atenderam, cada um, a 30% do público que procurou atendimento em T. Sabe-se ainda que A, B, C e D atenderam, respectivamente, 5%, 15%, 10% e 20% de pessoas com atendimento prioritário (idosos, deficientes, gestantes ou mães com crianças no colo, etc).
Selecionando-se ao acaso e com reposição cinco pessoas atendidas no balcão D, nesse mesmo dia, a probabilidade de exatamente duas terem sido do grupo de atendimento prioritário é de
Um dado é viciado de tal modo que a probabilidade de ocorrer face par é duas vezes mais provável do que ocorrer face ímpar. O dado é lançado duas vezes independentemente. Considere os seguintes eventos:
A = a soma dos pontos das faces é 6;
B = o número da face do primeiro dado é menor do que 3.
Nessas condições, a probabilidade de A, sabendo que ocorreu B, é
Para verificar e analisar o grau de eficiência de um
teste que poderia ajudar no retrocesso de uma doença
numa comunidade, uma equipe de biólogos aplicou–o
em um grupo de 500 ratos, para detectar a presença
dessa doença. Porém, o teste não é totalmente eficaz,
podendo existir ratos saudáveis com resultado positivo
e ratos doentes com resultado negativo. Sabe–se,
ainda, que 100 ratos possuem a doença, 20 ratos são
saudáveis com resultado positivo e 40 ratos são doentes
com resultado negativo.
Um rato foi escolhido ao caso, e verificou–se que seu
resultado deu negativo. A probabilidade de esse rato ser
saudável é

