Supondo que as probabilidades de ocorrência de dois eventos independentes sejam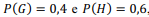
e considerando que 
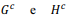denotem, respectivamente, os eventos complementares a G e H, assinale a opção correta.
Um auditor verificou que a probabilidade de determinado tipo de documento, quando feito em papel, ser preenchido corretamente é igual a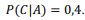 
. Por outro lado, a probabilidade de esse mesmo documento ser preenchido corretamente por meio de um aplicativo computacional é igual a 
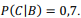Cada interessado deve optar por apenas uma das modalidades — papel ou aplicativo —, não sendo possível preencher o documento simultaneamente pelas duas formas.
Considerando a situação hipotética precedente e sabendo que o preenchimento por aplicativo computacional representa 90% dos casos, assinale a opção em que é apresentada a probabilidade de um processo ser preenchido corretamente, ou seja,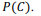 
Na Figura, representa-se a planificação de um dado cúbico, que será usado em um sorteio, que consiste em lançá-lo apenas três vezes. A pessoa que fará esses lançamentos ganhará um prêmio somente se, nesses três lançamentos, as faces SORTE e LANCE tiverem saído uma única vez em qualquer ordem.
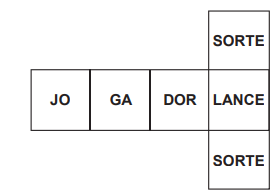
Considerando-se as seis faces do referido cubo equiprováveis, a probabilidade de essa pessoa ganhar o prêmio é igual a
Uma bandeja contém nove empadas de mesmo tamanho e aparência, mas com recheios diferentes: quatro são de frango, três são de palmito e duas, de camarão. Uma pessoa retira, ao acaso, duas dessas empadas.
A probabilidade de que ambas sejam de palmito é igual a:
Um aeroporto disponibiliza o serviço de transporte gratuito entre seus dois terminais utilizando os ônibus A e B, que partem simultaneamente, de hora em hora, de terminais diferentes. A distância entre os terminais é de 9000 metros, e o percurso total dos ônibus, de um terminal ao outro, é monitorado por um sistema de cinco câmeras que cobrem diferentes partes do trecho, conforme o esquema.
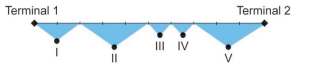
O alcance de cada uma das cinco câmeras é:
• câmera I: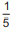 
do percurso;
• câmera II: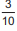 
do percurso;
• câmera III: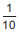 
do percurso;
• câmera IV: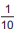 
do percurso;
• câmera V: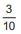 
do percurso.
Em determinado horário, o ônibus A parte do terminal 1 e realiza o percurso total com velocidade constante de 250 m/min; enquanto o ônibus B, que parte do terminal 2, realiza o percurso total com velocidade constante de 150 m/min.
Qual câmera registra o momento em que os ônibus A e B se encontram?
Para melhorar o fluxo de ônibus em uma avenida que tem dois semáforos, a prefeitura reduzirá o tempo em que cada sinal ficará vermelho, que atualmente é de 15 segundos a cada 60 segundos. Admita que o instante de chegada de um ônibus a cada semáforo é aleatório.
O engenheiro de tráfego da prefeitura calculou a probabilidade de um ônibus encontrar cada um deles vermelho, obtendo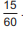 
A partir daí, estabeleceu uma mesma redução na quantidade do tempo, em segundo, em que cada sinal ficará vermelho, de maneira que a probabilidade de um ônibus encontrar ambos os sinais vermelhos numa mesma viagem seja igual a 
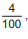considerando os eventos independentes.
Para isso, a redução do tempo em que o sinal ficará vermelho, em segundo, estabelecida pelo engenheiro foi de
J.P. gosta de usar gravatas e o faz diariamente para ir ao trabalho. Ele guarda as suas gravatas em um armário com todas elas penduradas em cabides. Ele possui 2 gravatas de bolinhas, 3 gravatas listradas, 3 gravatas com estampas diversas e 5 gravatas lisas. Ao pegar suas gravatas logo cedo após se vestir, J.P. tem dificuldade em ver com clareza as gravatas penduradas no armário e, às vezes, escolhe a gravata de forma aleatória. Em certa manhã, J.P. desejava usar uma gravata lisa. Suponha que J.P. pega uma gravata, de forma aleatória, e, ao perceber que não é lisa, faz outra retirada, mas sem devolver a primeira gravata ao armário. Na segunda retirada, J.P. obtém então a gravata desejada (lisa).
A probabilidade que o evento descrito ocorra é de (números percentuais aproximados):
Texto CG1A4-II
Certa instituição de fomento opera seus produtos por meio de apoio financeiro reembolsável ou não reembolsável. As formas de os clientes apresentarem suas propostas são: fluxo contínuo (mecanismo utilizado para o atendimento das demandas a qualquer momento); e chamadas públicas (ações estruturadas com seleção por meio de um processo de competição aberto ao público). Os instrumentos financeiros podem ser oferecidos diretamente pela instituição ou de forma indireta, por meio de agentes financeiros credenciados. Não existe restrição de um cliente ter acesso a um produto, seja este produto reembolsável ou não, seja pela forma de oferecimento direta ou indireta ou, ainda, pela forma de apresentação de sua proposta (fluxo contínuo ou chamada pública).
Na situação descrita no texto CG1A4-II, se um cliente escolher aleatoriamente entre as formas de acesso a um produto na instituição, a probabilidade de ele apresentar sua proposta na modalidade fluxo contínuo
A criptografia refere-se à construção e análise de protocolos que impedem terceiros de lerem mensagens privadas. Júlio César, imperador romano, utilizava um código para proteger as mensagens enviadas a seus generais. Assim, se a mensagem caísse em mãos inimigas, a informação não poderia ser compreendida. Nesse código, cada letra do alfabeto era substituída pela letra três posições à frente, ou seja, o “A” era substituído pelo “D”, o “B” pelo “E”, o “C” pelo “F”, e assim sucessivamente.
Disponível em: www.codifica.ibict.br. Acesso em: 15 out. 2019.
Qualquer código que tenha um padrão de substituição de letras como o descrito é considerado uma Cifra de César ou um Código de César. Note que, para decifrar uma Cifra de César, basta descobrir por qual letra o “A” foi substituído, pois isso define todas as demais substituições a serem feitas.
Uma mensagem, em um alfabeto de 26 letras, foi codificada usando uma Cifra de César. Considere a probabilidade de se descobrir, aleatoriamente, o padrão utilizado nessa codificação, e que uma tentativa frustrada deverá ser eliminada nas tentativas seguintes.
A probabilidade de se descobrir o padrão dessa Cifra de César apenas na terceira tentativa é dada por
Um hospital tem 7 médicos cardiologistas e 6 médicos neurologistas em seu quadro de funcionários. Para executar determinada atividade, a direção desse hospital formará uma equipe com 5 médicos, sendo, pelo menos, 3 cardiologistas.
A expressão numérica que representa o número máximo de maneiras distintas de formar essa equipe é
Em determinado órgão público, 10 servidores, trabalhando 8 horas por dia, atendem em média 300 pessoas por semana.
A idade média desses servidores é 40 anos. Para se somar a esse efetivo de atendimento ao público, foram contratados 6 novos servidores.
A partir da situação hipotética apresentada, julgue o item a seguir.
Se, após a contratação dos 6 novos servidores, 2 servidores forem aleatoriamente selecionados, a probabilidade de pelo menos um deles ser servidor antigo é igual a 3/8.
Ao voltar de férias, um escrivão esqueceu-se de um dos caracteres de sua senha do computador do trabalho. Apesar de não se recordar do caractere exato, ele se lembrava de que era uma letra e que podia ser ou não maiúscula.
Nesse caso hipotético, considerando-se que o sistema faça a distinção entre caracteres maiúsculos e minúsculos, a probabilidade de o escrivão acertar o caractere de sua senha em até quatro tentativas é de
Em uma caixa de munições de calibre 38, há 5 tipos de cartuchos com comprimentos distintos. Certo policial contabilizou: 14 munições do tipo Super Comp, de comprimento igual a 32,5 mm; 12 munições do tipo S&W, de comprimento igual a 30,5 mm; 8 munições do tipo Revolver Short, de comprimento igual a 27,9 mm; 10 munições do tipo Revolver Long, de comprimento igual a 35,6 mm; e 6 munições
do tipo Winchester, de comprimento igual a 40,4 mm.
Na situação descrita no texto 2A4-I, se uma munição for retirada da caixa, a probabilidade de essa munição ser do tipo S&W, sabendo-se que o comprimento do cartucho possui medida superior a 30 mm e inferior a 40 mm, será igual a
Em uma determinada cidade, a probabilidade de um morador, escolhido ao acaso, ter seguro de carro é de 80%. Em um determinado dia, cinco moradores são escolhidos ao acaso.
A probabilidade de que exatamente 3 deles tenham seguro de carro é, aproximadamente
Um setor de uma empresa é formado por 11 funcionários, dos quais 4 são estagiários e 7 são efetivos. Um grupo de
5 funcionários foi formado a partir de um sorteio aleatório entre os funcionários desse setor.
Qual é a probabilidade de o grupo formado possuir apenas um funcionário estagiário?
