Num cofrinho, há somente 50 moedas, sendo 20 delas de um real e as demais de cinquenta centavos. João retira aleatoriamente, desse cofre, duas moedas. A probabilidade de ambas as moedas retiradas por João serem de um mesmo valor corresponde a:
A probabilidade de sair soma 7 no lançamento de dois dados é:
Acerca de probabilidade e estatística, julgue o próximo item.
Considere que de uma urna com 10 bolas numeradas de 1 a 10, uma pessoa deva retirar, aleatoriamente, duas bolas ao mesmo tempo. Nesse caso, a probabilidade de que seja 12 a soma dos números das bolas retiradas é superior a 9%.
Considerando os números contidos no conjunto dos números naturais menores que 101, é correto afirmar que a probabilidade de escolhermos aleatoriamente o número 20 será:
Qual é a probabilidade de um dos cem números 1, 2, 3, 4...., 100 ser múltiplo de 6 e de 10 simultaneamente?
Considere que, em eventual sorteio de brindes, um nome tenha sido retirado, ao acaso, do interior de uma urna que continha os nomes de todos os familiares presentes no evento. Nessa situação, sabendo-se que o sorteado não é uma mulher da família Gödel, a probabilidade de ser uma mulher da família Russel será superior a 20%.
As pessoas que possuem o antígeno A e o antígeno B têm tipo sanguíneo AB. As que possuem apenas o antígeno A ou apenas o B têm tipo sanguíneo A e B, respectivamente. Pessoas que não possuem tais antígenos têm tipo sanguíneo O. Em testes de tipagem sanguínea com 280 pessoas, 100 pessoas tinham antígeno A, 85 pessoas tinham antígeno B e 140 não tinham nenhum antígeno.
Com base nesse caso hipotético, julgue o item a seguir.
Escolhendo-se ao acaso uma pessoa do teste, a chance de ela possuir o antígeno A é maior que 25%.
Considere todas as senhas formadas por três vogais maiúsculas. São exemplos dessas senhas: EEE, OIA e UAU.
Dentre todas as senhas desse tipo, escolhendo ao acaso uma delas, a probabilidade de que ela tenha duas letras iguais e uma diferente é de
A probabilidade de um assistente viajar é P(A)= 1/5, a de um técnico em contabilidade viajar é P(C)= 1/4 e a de um técnico em informática viajar é P(I)= 1/3.
A probabilidade de ao menos um deles viajar é:
Dos 10 administradores do CFO, 4 serão escolhidos para compor a comissão de licitação de compras diversas. A comissão terá um presidente, um vice-presidente, um secretário e um auditor, não podendo haver acúmulo de cargos. Jonas é um desses 10 administradores.
Com base nesse caso hipotético, julgue o item que se segue.
Considere-se que tenham sido listadas todas as possíveis comissões e que cada uma delas tenha sido escrita em um pedaço de papel, dobrado e colocado em uma urna para uma escolha aleatória. Nesse caso, a probabilidade de se escolher uma comissão em que Jonas não ocupe nenhum dos 4 cargos é superior a 65%.
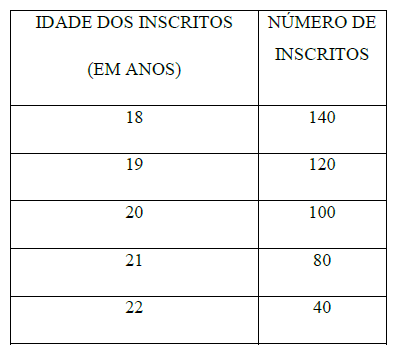
A tabela abaixo apresenta dados coletados nas inscrições dos candidatos de um concurso, de acordo com a idade de cada um.
Se escolhermos aleatoriamente apenas um desses candidatos, a probabilidade de ele ter 21 ou 22 anos é:
Um grupo de estudantes do Colégio DELTA recebe forte estímulo para a participação, no final do ano letivo de 2018, em diversas Olimpíadas intelectuais. Há uma previsão de que 44 estudantes participem da Olimpíada de Matemática, 38 na de Física e 26 em ambas. Por outro lado, do grupo, os demais 14 estudantes participarão de outras Olimpíadas. Uma vez confirmada a participação dos estudantes nas olimpíadas em foco, é correto afirmar que a probabilidade de estudantes do grupo participarem de apenas uma das olimpíadas de Matemática ou Física é
Em uma população formada por indivíduos que se encontram empregados, observa-se que 40% deles têm um salário superior a 10 salários mínimos. Para desenvolver um estudo, é extraída uma amostra aleatória de 3 indivíduos desta população com reposição. A probabilidade de que mais que 1 indivíduo desta amostra não tenha um salário superior a 10 salários mínimos é de
Dois tabuleiros de xadrez serão utilizados para a criação de um jogo de sorteio. Inicialmente as linhas e as colunas desses tabuleiros foram numeradas conforme a figura 1. Em seguida, cada casa do tabuleiro será associada ao número que é a soma dos números da linha e da coluna dessa casa. Participarão do sorteio 5 pessoas, e cada uma delas deverá escolher uma das casas do tabuleiro. Em seguida, outra pessoa, chamada juiz, que não tenha visto a escolha dos 5 jogadores, deverá escolher, no outro tabuleiro, uma casa qualquer e realizar a soma da linha e da coluna relativas a essa casa. Será considerado ganhador aquele que tenha escolhido a casa cuja soma do número da linha com o número da coluna coincida com a soma do número da linha com o número da coluna da escolha do juiz.
Se os 5 jogadores escolherem as casas indicadas pelas letras A, B, C, D e E, conforme a figura 2, o jogador que tem maior probabilidade de vencer o sorteio é o que escolher a casa com a letra
Um procedimento muito comum em provas objetivas de concursos, quando o candidato não consegue resolver uma determinada questão, é “escolher aleatoriamente" uma das opções possíveis.
Se o candidato sabe resolver a questão, então ele tem 100% de chance de escolher a opção correta.
Considere um exame em que, para cada questão, existem quatro opções de resposta e apenas uma delas é a correta. Um determinado candidato sabe 70% das respostas desse exame e respondeu corretamente a uma determinada questão.
A probabilidade de este candidato ter “escolhido aleatoriamente" a opção correta dessa questão é