Em um jogo bingo são sorteados, sem reposição, números de um a trinta. Qual a probabilidade do primeiro número sorteado ser par e primo?
Em uma sala do último ano do ensino médio com 50 alunos, sendo 28 meninas, foi feita uma pesquisa sobre o curso que pretendiam fazer na faculdade. Entre os 6 alunos que responderam que pretendiam fazer Arquitetura estavam apenas 2 meninas.
Tomando ao acaso um desses alunos, qual é a probabilidade de que, sendo menina, pretenda fazer Arquitetura?
A probabilidade de sucesso em uma prova de campo é a nona parte da probabilidade de fracasso. Provas sucessivas e independentes são realizadas até que o sucesso ocorra pela primeira vez. Nessas circunstâncias, o número esperado de fracassos que deverão ocorrer até que se verifique o primeiro sucesso é igual a
Manu e Ítalo estão brincando com um jogo. Nele, cada participante recebe 10 fichas com números, que devem ser embaralhadas e sorteadas durante cinco rodadas. Após o sorteio, a ficha sorteada volta para o monte para participar da próxima rodada. Os participantes marcam 1 ponto se sortear um número:
• Par na 1ª rodada;
• Ímpar na 2ª rodada;
• Que contém o algarismo 9 na 3ª rodada;
• Que termina com o algarismo 1 na 4ª rodada;
• Cuja soma dos algarismos seja igual a 17 na 5ª rodada. Veja a seguir as fichas que cada participante recebe:
Qual é a probabilidade de um participante fazer um ponto em cada rodada?
Em uma urna foram colocadas sete bolas vermelhas, quatro bolas azuis, três bolas verdes e duas bolas brancas. Se forem sorteadas 2 bolas, uma de cada vez, sem reposição, a probabilidade da primeira a ser sorteada ser verde e última, ser branca é:
Para uma comissão, necessitam‐se de 4 técnicos e 2 engenheiros. Há disponíveis 6 técnicos e 5 engenheiros, entre os últimos, Abel.
Com base nesse caso hipotético, julgue o item seguinte.
Escolhendo‐se aleatoriamente, a probabilidade de Abel estar na comissão é maior que 30%.
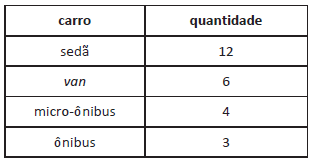
Para se percorrer um trajeto, existem alguns carros disponíveis, conforme a tabela a seguir.
As vans e os ônibus estão com freios novos, os sedãs e os micro−ônibus estão com freios gastos.
Sabendo−se, nessa situação hipotética, que um motorista está dirigindo um veículo com freios novos, a probabilidade de que seja uma van é igual a
Uma moeda é lançada quatro vezes. A probabilidade de saírem mais caras do que coroas é de
Um baralho possui 52 cartas, que incluem 4 ases. A chance de escolher, ao acaso, 2 ases do baralho é um valor
Ao escolher aleatoriamente um dos anagramas da palavra Brasil qual é, aproximadamente, a probabilidade de sua primeira letra ser consoante?
Um ponto P(x, y) é escolhido aleatoriamente no círculo de raio 1, centrado na origem.
Seja R a região definida por R = {(x, y) ∈ IR2,|x − y| ≤ 1}.
A probabilidade de o ponto P pertencer à região R é
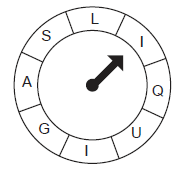
A Figura a seguir mostra um jogo eletrônico no qual, a cada jogada, a seta, após ser girada, para, aleatoriamente e com igual probabilidade, em qualquer uma das oito casas com as letras da palavra LIQUIGÁS.
Um jogador só é vencedor se, em duas jogadas consecutivas, a seta apontar para letras iguais.
A probabilidade de um jogador ser vencedor, fazendo apenas duas jogadas, é igual a
Afim de celebrar seu milésimo contrato, uma empresa de telefonia realizará um sorteio de um carro novo entre seus clientes. Quanto mais contratos em seu nome um cliente possui, maiores serão as chances deste cliente ser sorteado. Caio, um de seus clientes mais importantes, possui um número x de contratos que equivale a quantidade de números naturais menores que dez. Podemos afirmar que a probabilidade de Caio ser sorteado será:
Cada uma das diferentes letras gregas da palavra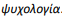 
foi escrita em uma bola e todas a bolas foram colocadas em uma urna, retirando-se, em seguida, sem reposição, duas delas.
Com base nesse caso hipotético, assinale a alternativa que apresenta a probabilidade de as inscrições da letra grega psi e da letra grega ghama não se encontrarem em nenhuma das duas bolas.
Considere 2 urnas: na primeira urna há 1 bola branca e 1 bola preta; na segunda urna, há 1 bola branca e 2 pretas. Uma bola é selecionada aleatoriamente da urna 1 e colocada na urna 2. Em seguida, uma bola é selecionada, também aleatoriamente, da urna 2. Qual a probabilidade de que a bola selecionada na urna 2 seja branca?
