Um sorteio será realizado utilizando para as apostas um cartão contendo números de 1 a 15 e cada apostador poderá escolher 5 números para o sorteio. A probabilidade de um apostador ganhar o sorteio é, aproximadamente:
Sabendo que x e y são inteiros e positivos e que x + y = 5, assinale a alternativa que apresenta a probabilidade de x ser 4.
De uma cervejeira que tem em seu interior três cervejas da marca A, quatro cervejas da marca B e cinco cervejas da marca C, foram retiradas duas cervejas, sem se observar a marca.
Com base nesse caso hipotético, assinale a alternativa que apresenta a probabilidade de as duas cervejas serem da mesma marca.
Para o sorteio de amigo secreto, Maria gostaria de tirar uma menina. Sabendo que todos os 42 alunos de sua sala participariam e que contando com ela, a população de meninas era o dobro da população de meninos, quais as chances de Maria tirar como amigo secreto um menino?
Para o sorteio de amigo secreto, Maria gostaria de tirar uma menina. Sabendo que todos os 42 alunos de sua sala participariam e que contando com ela, a população de meninas era o dobro da população de meninos, quais as chances de Maria tirar como amigo secreto um menino?
As 20 vagas de um estacionamento são organizadas em 4 fileiras de 5 vagas cada, sendo as vagas da primeira fileira numeradas de um a cinco [1 a 5], da segunda fileira de seis a dez [6 a 10] e assim sucessivamente. Quatro veículos entram no estacionamento vazio. A probabilidade de que os quatros veículos estacionem em vagas numeradas com números primos, e em fileiras distintas é
Os indivíduos S1, S2, S3 e S4, suspeitos da prática de um ilícito penal, foram interrogados, isoladamente, nessa mesma ordem. No depoimento, com relação à responsabilização pela prática do ilícito, S1 disse que S2 mentiria; S2 disse que S3 mentiria; S3 disse que S4 mentiria.
A partir dessa situação, julgue o item a seguir.
Considerando que a conclusão ao final do interrogatório tenha sido a de que apenas dois deles mentiram, mas que não fora possível identificá-los, escolhendo-se ao acaso dois entre os quatro para novos depoimentos, a probabilidade de apenas um deles ter mentido no primeiro interrogatório é superior a 0,5.
Um agente de fiscalização e orientação visitou sete escolas, quatro empresas e três laboratórios. Depois, apresentou um relatório de fiscalização para cada estabelecimento que visitou.
Com base nessa situação hipotética, julgue o item a seguir.
Sabendo-se que a metade dos relatórios apresentaram problemas nos estabelecimentos visitados, então a probabilidade de haver problema em algum relatório referente a uma escola é maior que 99%.
Ao sortear duas cartas consecutivamente e sem reposição em um baralho completo, qual é a probabilidade de serem retirados um oito de copas e um seis de ouro? (Considerar o baralho completo com 52 cartaz e cada naipe com 13 cartaz)
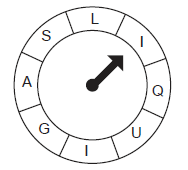
A Figura a seguir mostra um jogo eletrônico no qual, a cada jogada, a seta, após ser girada, para, aleatoriamente e com igual probabilidade, em qualquer uma das oito casas com as letras da palavra LIQUIGÁS.
Um jogador só é vencedor se, em duas jogadas consecutivas, a seta apontar para letras iguais.
A probabilidade de um jogador ser vencedor, fazendo apenas duas jogadas, é igual a
Uma aposta é feita em um jogo de sorte. Um jogador para ganhar a rodada final terá que atirar uma moeda e um dado é jogado. O jogador ganhará a premiação se o resultado da rodada for cara para a moeda e ser o número 4 no dado. Marque a alternativa que apresenta a probabilidade aproximada do jogador ganhar a rodada.
Dados os conjuntos A = {1, 2, 3} e B = {4, 5, 6, 7}, João escolhe ao acaso um elemento de cada um deles.
A probabilidade de que o produto dos dois elementos escolhidos seja um número par é:
Numa urna há somente 8 bolas azuis numeradas de 1 a 8 e 12 bolas verdes numeradas de 9 a 20. A probabilidade de sortearmos uma única bola dessa urna e ela ter um número par, sabendo que ela é azul,é
Considere que, em eventual sorteio de brindes, um nome tenha sido retirado, ao acaso, do interior de uma urna que continha os nomes de todos os familiares presentes no evento. Nessa situação, sabendo-se que o sorteado não é uma mulher da família Gödel, a probabilidade de ser uma mulher da família Russel será superior a 20%.
A probabilidade de um assistente viajar é P = 1/5, a de um técnico em contabilidade viajar é P(C) = 1/4 e a de um técnico em informática viajar é P(I) = 1/3.
A probabilidade de ao menos um deles viajar é: