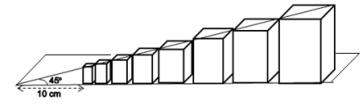
Um professor de matemática tirou o final de semana para organizar sua estante de livros e em uma das prateleiras ele usou a seguinte formação: foram dispostos oito livros, um ao lado do outro, de acordo com suas respectivas espessuras e alturas, de modo que um sempre tivesse o dobro da espessura do outro e o da frente seja sempre maior que o de trás, formando com a base da prateleira onde estavam, um triangulo retângulo com um ângulo de 45º, como expresso na figura abaixo. Qual a altura, em metros, do maior livro, sabendo que o menor livro mede 0,2cm de espessura?
Dados: use √3 = 1,7.
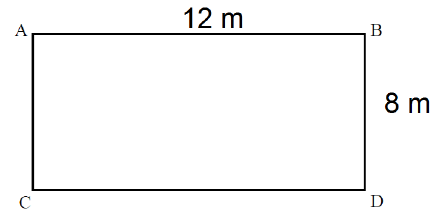
Joelma vai utilizar uma tela de 6,4 metros de comprimento para cercar uma pequena horta com formato retangular no quintal de sua casa, onde irá plantar algumas hortaliças. É necessário reservar pelo menos 0,04 m2 da horta para cada planta. Se Joelma construir a cerca de modo que a horta tenha a maior área possível, quantas plantas, no máximo, poderão ser cultivadas nessa horta?
Atenção: Para responder à questão, considere o texto abaixo.
Ao explicar para outra pessoa um trajeto de carro, nos valemos de instruções como
vire à esquerda na primeira rua que der mão, vire à direita no farol e diversas outras.
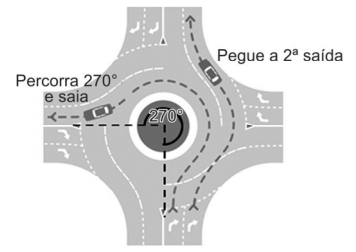
Se o caminho passar por uma rotatória, pode-se descrever essa passagem de, pelo menos, duas maneiras:
− pegue a 2ª saída;
− percorra 270° e saia.
Considere a figura.
Veja a seguir a representação de uma região da cidade de Palmas, capital do estado do Tocantins:
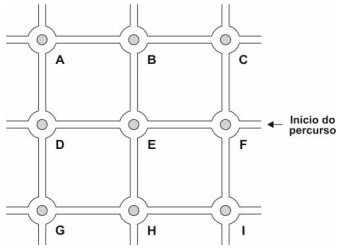
As 6 avenidas exibidas são de mão dupla, os 9 cruzamentos destacados se dão por meio de rotatórias, as quais foram nomeadas por A, B, C, ... I. Em cada uma das 9 rotatórias destacadas, há apenas 3 saídas diferentes daquela em que o carro entrou (a 4ª saída é a mesma por onde o carro entrou).
Um carro se encontra no ponto destacado na figura, prestes a entrar na rotatória F. Ele irá seguir a sequência de instruções:
− percorra 180° na rotatória F, saia e siga até a próxima rotatória;
− pegue a 3ª saída na rotatória e siga até a próxima rotatória;
− percorra 90° na rotatória, saia e siga até a próxima rotatória.
Após seguir a última instrução, o carro chegará à rotatória
Na casa de Vítor, está ocorrendo um fenômeno, não raro, mas indesejável. As cerâmicas do piso da sala estão estufando e, consequentemente, se desprendendo do chão. Com a intenção de avaliar e calcular os estragos e gastos, Vítor realizou várias medidas, chegando às seguintes conclusões:
• a área total do chão da sala de sua casa é igual a 30 m2;
• 62% do piso da sala não foi comprometido e poderá ser reaproveitado;
• as cerâmicas que serão utilizadas para reposição são vendidas em caixas com 5 cerâmicas cada. A área total de cada caixa é igual a 8 000 cm2.
Desconsiderando o espaçamento entre as cerâmicas, o número mínimo de peças de cerâmica que Vítor deverá comprar para reparar os estragos causados no piso de sua sala é igual
A figura a seguir mostra o gráfico da função f(x) = log2x e os pontos:
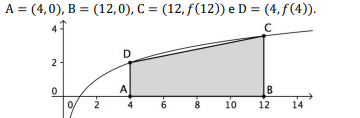
Considerando f(3) = 1,585, a área do quadrilátero ABCD é igual a
Uma pizzaria serve uma pizza circular gigante dividida em oito fatias, com borda de catupiry na circunferência externa, medindo 15 em a borda de cada fatia.
Adote π = 3
O valor da área dessa pizza é:
A diagonal do octaedro regular de lado L é
Ainda com base no terreno apresentando anteriormente, é correto afirmar que a soma de todos os seus lados é igual a:
A figura seguinte mostra a planta baixa de um condomínio. O terreno ocupado pelo condomínio é um quadrado de lados que mede 60 m. Nesse condomínio, as áreas indicadas por E1, E2 e E3 correspondem aos locais onde estão construídos os prédios residenciais, e as regiões em branco correspondem às vias de livre circulação para pedestres e veículos.
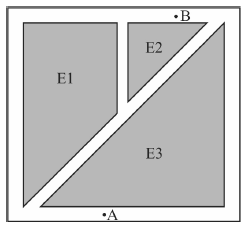
A partir da figura e das informações precedentes, julgue o item a seguir, considerando que a área de E2 seja igual a 200 m2 .
Situação hipotética: Dois policiais devem ir do ponto A ao B, pelas vias de livre circulação, cada um deles fazendo um caminho diferente, sem passar duas vezes pelo mesmo local. Toda vez que os dois policiais chegarem ao ponto B, conta-se como realizado um trajeto. Assertiva: Nessa situação, a quantidade de trajetos distintos que os policiais poderão percorrer é inferior a 40.
O comprimento, em cm, da circunferência que contém os pontos C1, C2 e C3 é igual a
Na figura a seguir, temos a representação de uma transformação T no plano, de polígonos localizados nos 1º e 2º quadrantes em polígonos localizados nos 3º e 4º quadrantes. A transformação gera polígonos semelhantes aos iniciais.

A matriz de transformação correspondente a T é
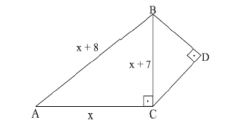
Na figura a seguir, BCD é um triângulo retângulo isósceles.
Logo, o lado BD mede
Um triângulo retângulo com a altura sendo 4 vezes maior do que a sua base tem área igual a 8 cm2. Sabendo que o ângulo reto está situado entre a altura e a base e que um cone de revolução é feito girando o triângulo entorno do eixo segundo à direção da altura, assinale a alternativa que apresenta o valor aproximado do volume, em litros, do sólido formado.
Considere π = 3,14.
Um triângulo retângulo tem seus vértices nos pontos de coordenadas cartesianas (0 , 0) , (3 , 0) e (0 , 4). O perímetro deste triângulo mede:
A figura a seguir exibe um mapa em que três ruas paralelas entre si são cortadas por outras três ruas, paralelas entre si e perpendiculares às três primeiras. As setas indicam os sentidos de circulação permitidos em cada rua.
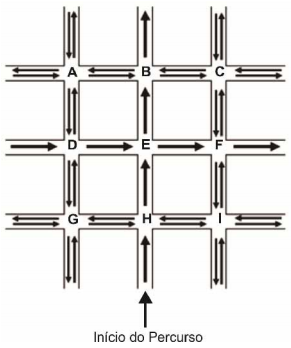
Os 9 cruzamentos entre essas vias foram nomeados por A, B, C, ... , I, como pode ser visto na figura. Um carro se encontra percorrendo a via destacada na figura, antes de entrar no cruzamento H. Ele deve seguir a sequência de instruções (após cada instrução, o carro percorre todo o quarteirão, até atingir o cruzamento e executar a instrução seguinte):
− 2ª rua à esquerda;
− 1ª rua à esquerda;
− 1ª rua à esquerda;
− 1ª rua à direita.
Sabendo que as instruções se referem sempre às ruas de conversão permitida (por exemplo, a instrução “1ª rua à esquerda" deve ser interpretada como “1ª rua à esquerda cuja conversão é permitida"), a pessoa atingirá, após seguir a última instrução e percorrer o quarteirão, o cruzamento