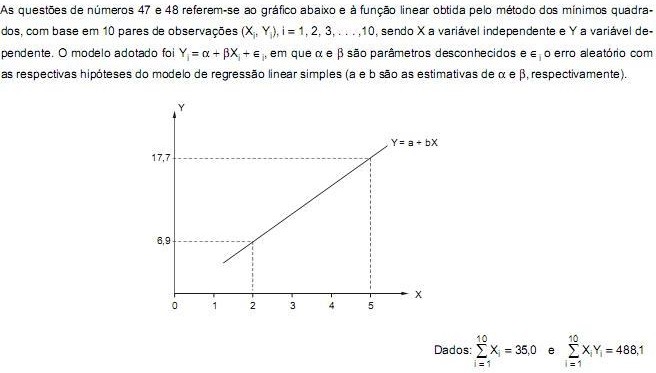
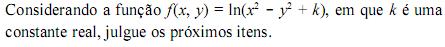Considere duas variáveis aleatórias discretas X e Y, ambas com distribuição binomial. Sabe-se que: X: b (2, p) e Y: b (4, p). Se P (X = 1) =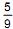 
então P (Y = 1) é
Se o modelo de Séries Temporais dado por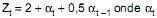 
é o ruído branco de média zero e desvio padrão 2, tem função de autocorrelação dada por ? (t), t = 1,2,3, .... , então o valor de ? (1) é
Um estudo sobre salários associados ao estado civil dos indivíduos de certa comunidade revelou que a proporção de indivíduos:
I. solteiros é de 0,4.
II. que recebem até 5 salários mínimos é de 0,3.
III. que recebem entre 5 (exclusive) e 10 (inclusive) salários mínimos é de 0,5.
IV. que recebem até 5 salários mínimos entre os solteiros é de 0,3.
V. que são não solteiros dentre os que recebem mais do que 10 salários mínimos é de 0,8.
Um indivíduo é selecionado ao acaso dessa comunidade. A probabilidade de ele ser solteiro e ganhar entre 5 (exclusive) e 10 (inclusive) salários mínimos é
Utilizando a equação da reta obtida pelo método dos mínimos quadrados, obtém-se que o valor da previsão de Y para X = 7 é igual a
Em uma fábrica existem 3 máquinas A, B e C que produzem diariamente 10.000 peças. Sabe-se que A, B e C produzem, respectivamente, 2000, 5000 e 3000 peças. Da produção de A, B e C, respectivamente, 5%,10% e 20% são defeituosas. Seleciona-se uma peça ao acaso e verifica-se que é defeituosa. A probabilidade dela ser proveniente da máquina C é
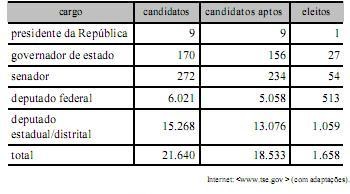
Com base na tabela acima, referente às eleições de 2010, que apresenta a quantidade de candidatos para os cargos de presidente da República, governador de estado, senador, deputado federal e deputado estadual/distrital, bem como a quantidade de candidatos considerados aptos pela justiça eleitoral e o total de eleitos para cada cargo pretendido, julgue os itens a seguir.
A quantidade de candidatos a deputado federal, estadual ou distrital é superior a 100 vezes a quantidade de candidatos ao Senado.
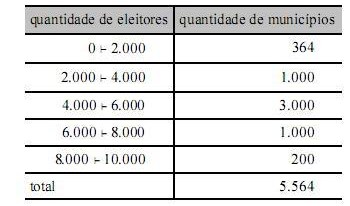
A tabela acima apresenta uma distribuição hipotética das quantidades de eleitores que não votaram no segundo turno da eleição para presidente da República bem como os números de municípios em que essas quantidades ocorreram. Com base nessa tabela, julgue os itens segunites, relativos à análise exploratória de dados.
A moda da distribuição se encontra no mesmo intervalo de classe que contempla a mediana e a média.
A tabela acima apresenta uma distribuição hipotética das quantidades de eleitores que não votaram no segundo turno da eleição para presidente da República bem como os números de municípios em que essas quantidades ocorreram. Com base nessa tabela, julgue os itens segunites, relativos à análise exploratória de dados.
Na tabela de frequências, o uso de intervalos de classe permite concluir que a variável em questão é contínua.
Julgue os itens que se seguem, referentes às técnicas de amostragem e de inferência estatística.
Uma pesquisa de âmbito nacional para obter a intenção dos brasileiros na eleição para presidente da República pode ser feita com base em uma amostragem que considera pelo menos três estágios: por região, por estado e por município.
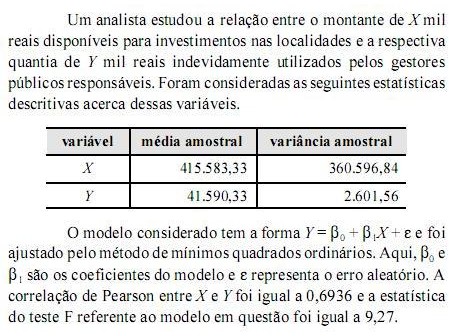
Com base nessas informações, julgue os próximos itens, relativos a correlação, regressão e distribuições conjuntas.
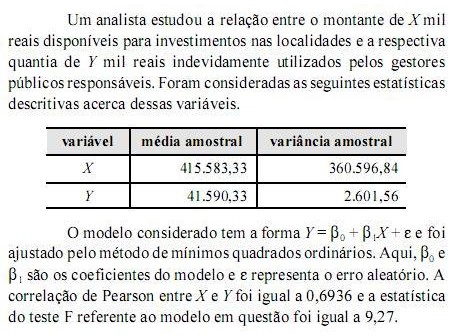
Com base nessas informações, julgue os próximos itens, relativos a correlação, regressão e distribuições conjuntas.
Ao se efetuar a operação Z = 1.000 (X Y), a estimativa da média de Z será superior a R$ 360 milhões e inferior a R$ 380 milhões.
Com relação ao algoritmo EM (expectation-maximization), julgue os itens que se seguem.
Se X e Y forem variáveis aleatórias independentes e se 2 for um parâmetro da distribuição de X, em que X é uma variável não observada, então o algoritmo EM será um método adequado para se obter estimativas de máxima verossimilhança para 2.
A tabela acima apresenta a distribuição percentual da população brasileira em área rural e urbana, nos períodos de 1940 a 2000. A coluna êxodo rural mostra o percentual das pessoas que migraram do campo para a área urbana. Com base nessas informações, julgue os itens subsequentes.
Se o êxodo rural na década 2000-2010 permaneceu igual ao da década anterior, então o percentual da população brasileira residente em área rural em 2010 foi igual 8,77%.
