Uma população X tem uma função densidade dada por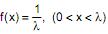 
Por meio de uma amostra aleatória de 10 elementos de X, obteve-se, pelo método da máxima verossimilhança, uma estimativa para a média de X igual a 4,5. Com base neste resultado, tem-se que a respectiva estimativa da variância de X é igual a
Os preços unitários de venda de um determinado equipamento no mercado estão distribuídos conforme representação do histograma abaixo. No eixo das ordenadas constam as respectivas densidades de frequências em (R$ 1.000,00) -1. Define-se densidade de frequência de um intervalo de classe como sendo o quociente da divisão da respectiva frequência relativa pela correspondente amplitude do intervalo.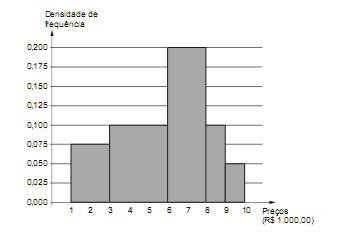 
Considerando os intervalos de classe fechados à esquerda e abertos à direita, obtém-se que a porcentagem dos preços unitários, que são iguais ou superiores a R$ 3.000,00 e inferiores a R$ 8.000,00, corresponde a
Atenção: Considere as informações a seguir para responder às questões de números 86 a 88.
A distribuição dos salários dos 1000 funcionários da companhia A, em número de salários mínimos, está apresentada na tabela
abaixo: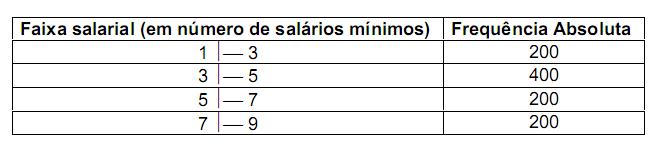 
A média dos salários, calculada supondo-se que todos os valores dentro de uma faixa salarial tenham seus valores iguais ao ponto médio desta faixa, em número de salários mínimos, é igual a
A questão refere-se a Estatística.
Uma urna contém 3 bolas brancas, 4 pretas e 3 amarelas. Desta urna, três bolas são selecionadas ao acaso e com reposição. A probabilidade de que, entre as 3 selecionadas, no máximo duas sejam pretas é
Considere a distribuição conjunta de duas variáveis aleatórias
discretas X e Y dada pela expressão seguinte: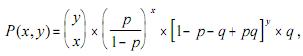
em que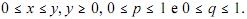 
Julgue os seguintes itens a respeito dessa distribuição.
O valor esperado do produto XY pode ser obtido da expressão
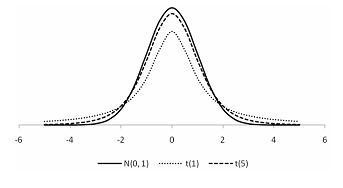
O gráfico acima mostra a função de densidade da distribuição normal padrão N(0, 1) e t(1) e t(5), que representam, respectivamente, as densidades da distribuição t de Student com 1 e 5 graus de liberdade. Com base nesse gráfico, julgue o próximo item.
A distribuição N(0, 1) possui variância unitária, a t(5) possui variância igual a 5/3, e a variância da distribuição t-Student com 1 grau de liberdade é indefinida.
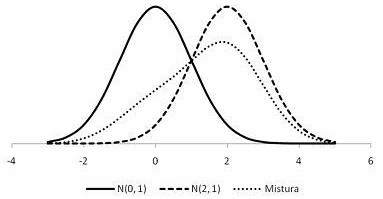
A figura acima mostra a função densidade da distribuição normal
padrão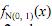 
, a função densidade da distribuição normal
com média 2 e desvio padrão 1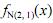 
, e a combinação entre
elas 
Julgue os itens que se
seguem, com relação a essas funções.
A variância da distribuição da combinação f ( x) é inferior a 1,5.
A partir da figura acima, que ilustra a evolução temporal
(de janeiro/1959 a dezembro/1997) dos níveis mensais de
concentração de 
registrados em determinada localidade, julgue
os itens de 40 a 42.
O modelo ARMA (p,q ), em que p, q 
6, possibilita ajustar a série temporal original.
Julgue os itens que se seguem, a respeito de análise de dados
discretos.
Considere que uma amostra de tamanho n seja representada por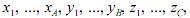 
em que x, y e z são as unidades amostrais retiradas de três grupos distintos X, Y e Z, e n = A + B + C. Nessa situação, sabendo-se que a média geral 
então a média aritmética das médias por grupo será igual à média geral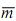 
somente se A = B = C .
Em relação aos métodos numéricos, julgue os itens que se seguem.
Os métodos numéricos de integração permitem obter a função primitiva do integrando, mas não permitem o cálculo numérico de integrais definidas.
Considere o modelo de regressão linear simples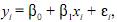 
em que i = 1, 2,
, n; y represente a variável resposta; x seja a
variável independente;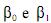 
sejam constantes; e as variáveis
aleatórias 
sejam independentes e normais com média zero
e variância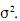 
Acerca desse modelo, julgue os seguintes itens.
Para testar se o coeficiente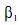 
é nulo, é correto o uso da razão QMReg/QMRes , que, sob a hipótese nula 
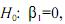segue distribuição F de Snedecor com parâmetros 1 e n - 2, em que QMReg e QMRes são, respectivamente, os quadrados médios da regressão e residual.
No que concerne aos planos amostrais, julgue os itens a seguir.
No plano amostral por conglomerados, o coeficiente de correlação intraclasse mede o quanto os elementos dentro dos conglomerados são similares, sendo que, quanto maior for o coeficiente, mais heterogêneos são os conglomerados e melhores serão os resultados obtidos por meio desse tipo de plano amostral.
Considere que a população de determinado país, no instante inicial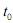
= 0, seja igual a 
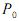> 0, que essa população cresça à taxa anual de
2% e que as taxas de imigração e de emigração sejam desprezíveis.
Com base nessas informações, julgue os próximos itens.
Em 50 anos, contados a partir do instante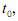 
o número de habitantes desse país será superior a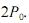 
Com relação aos testes de hipóteses paramétricos, julgue os itens
subsecutivos.
Considere que duas amostras independentes, de tamanhos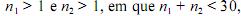 
foram retiradas de duas populações normais com variâncias desconhecidas e diferentes. Nessa situação, é correto afirmar que a estatística do teste dada pela diferença padronizada das médias aritméticas dessas duas amostras segue, sob a hipótese nula, distribuição t de Student com 
2 graus de liberdade.
Estão em uma sala quatro pessoas que foram convocadas
por um juiz: duas delas efetivamente testemunharão; as outras se
recusarão a testemunhar acerca de determinado fato. O juiz chamará
essas pessoas, uma a uma, para outra sala, mediante sorteio
aleatório. Considere que X seja a variável aleatória que indica o
número de pessoas chamadas até se encontrar a primeira pessoa
disposta a testemunhar.
Com base nessa situação hipotética, julgue os itens que se seguem.
A variável aleatória X segue uma distribuição geométrica com parâmetro p = 0,5.
