Julgue os itens subsecutivos, acerca de análise multivariada e distribuições conjuntas.
Para dados não correlacionados, a distância de Mahalanobis é proporcional à distância euclidiana.
Considerando a série temporal  , em que T é o
, em que T é o
componente de tendência, S é o componente de sazonalidade e e é
um componente aleatório de média 0 e variância constante, julgue
os itens a seguir.
Um modelo de regressão com tendência polinomial e variáveis dummies para descrever a componente S pode ser usado corretamente para a estimação dos componentes da série temporal 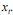 .
.
Se, em determinada fábrica, 10% das peças produzidas são
defeituosas, então, para fins de controle de qualidade, uma
distribuição binomial negativa deve ser usada na situação em que
se deseje, em uma amostra aleatória simples com reposição, obter a probabilidade de a terceira peça defeituosa ocorrer na décima retirada.
No que concerne a diagnóstico em análises de regressão, julgue o item a seguir.
Uma observação pode ser discrepante e não influente.
Os procedimentos estatísticos paramétricos incluem
a estimação da densidade da distribuição Gama(a, b), estimando-se os parâmetros a e b pelo método dos momentos.
Considerando que W seja um estimador pontual de um parâmetro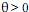 de uma distribuição D, julgue os itens a seguir.
de uma distribuição D, julgue os itens a seguir.
Independentemente da forma da distribuição D, o estimador W produzido pelo método dos momentos não é viciado para  .
.
Julgue os itens que se seguem, acerca de definições da teoria
estatística.
O erro do tipo II de um teste de hipóteses ocorre quando se rejeita uma hipótese nula que é verdadeira.
Acerca da teoria de probabilidades, julgue os itens subsecutivos.
A distribuição uniforme contínua em [0, 1] é um caso degenerado da distribuição beta.
A respeito das medidas de assimetria e curtose, julgue os próximos
itens.
A curtose de uma distribuição correspondente a um conjunto de dados X com n elementos e média aritmetica  pode ser corretamente calculada a partir da expressão abaixo. No caso em que X tem distribuição normal, a curtose é zero.
pode ser corretamente calculada a partir da expressão abaixo. No caso em que X tem distribuição normal, a curtose é zero.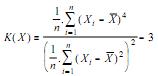
Com relação a representações gráficas, julgue os itens de 3 a 7.
O gráfico de perfil de médias mostrado na figura abaixo sugere uma interação entre os grupos A e B na amostra em questão.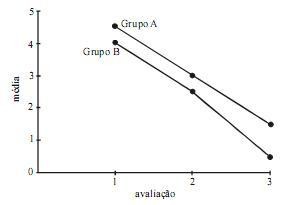
Considerando a série temporal 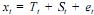 , em que T é o
, em que T é o
componente de tendência, S é o componente de sazonalidade e e é
um componente aleatório de média 0 e variância constante, julgue
os itens a seguir.
O método de suavização por médias móveis não é aplicável para essa situação, pois a série 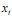 possui sazonalidade.
possui sazonalidade.
A função geratriz de momentos de uma variável aleatória X com distribuição Gama, cujos parâmetros são os números reais a e 0 = ß > 1 a é dada por 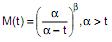
Com base nessa função, é verdade que a função geratriz de momentos de uma variável aleatória exponencial com parâmetro a > 0, para t < a , é:
Sejam f(k), k=1,2,3,... e h(k), k=1,2,3,..., respectivamente, as funções de autocorrelação e autocorrelação parcial de um processo ARMA(p,q).
Sabe-se que:
I. f(k) ≠ 0, para k=1 e 2, e é igual a zero para outros valores de k.
II. h(k) é dominada por uma mistura de exponenciais e senoides amortecidas.
As características (I) e (II) nos levam a identificar para p e q, respectivamente, os valores
A população das medidas dos comprimentos de um tipo de cabo é considerada normalmente distribuída e de tamanho infinito. Seja µ a média desta população com uma variância populacional igual a 2,56 m2. Uma amostra aleatória de 64 cabos apresentou um intervalo de confiança de (1-a), em metros, igual a [61,6 ; 62,4]. Se na distribuição normal padrão (Z) a probabilidade P(z> z)=a ⁄ 2 , então z é igual a


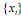 é estacionária para qualquer valor
é estacionária para qualquer valor 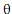 .
.