Em um estudo clínico utilizou-se um modelo de regressão logística
em que y é a variável resposta, como preditor linear, a expressão
a + bx + cz, em que x = 0 para o grupo placebo e x = 1 para o grupo
de tratamento; z é uma medida de colesterol (em escala de 0 a 5)
antes do início do tratamento. Com base nessas informações, julgue
os itens subsequentes
Considerando-se exp(c) = 0,7, se x se mantiver constante, então o aumento em uma unidade na medida de colesterol implicará em redução de 30% na chance de sucesso (y = 1).
Em relação ao processo estocástico X =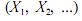 
julgue os
seguintes itens.
O processo estocástico X será estacionário se sua variância for decrescente no tempo, como em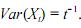 
Julgue os itens subsecutivos, relativos a programação linear (PL).
Nas sucessivas iterações do método simplex, nem sempre é mantida a viabilidade das novas soluções, garantindo-se, somente, que a solução final seja viável.
Com relação a indicadores demográficos, julgue os itens a seguir.
O índice de Myers é uma medida usada para avaliar a qualidade de declarações de idade em dados demográficos, como, por exemplo, as idades reportadas por indivíduos entrevistados pelo censo do IBGE.
Considerando que X, Y e Z sejam variáveis aleatórias, que a seja
uma constante não nula e que E, Md, Var, Cov,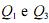 
denotem,
respectivamente, esperança, mediana, variância, covariância,
primeiro quartil e terceiro quartil, julgue os itens a seguir.
Md(X + a) = Md(X).
Julgue os itens subsequentes, relativos a um estimador T de um
parâmetro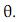 
Se, em probabilidade, T convergir para E(T), então T será consistente.
Baseando-se numa amostra aleatória de 30 observações, foi ajustada a equação de regressão associada ao modelo linear
y = a+bx+e, com soma de quadrados da regressão igual a 1650 e soma de quadrados total 2350. O valor da estatística F para
testar a hipótese H0 : b = 0 contra H1 : b ≠ 0 é dado por
Atenção: Para resolver às questões de 67 a 70, considere as seguintes informações: Se Z tem distribuição normal padrão, então: P(Z < 1) = 0,841; P(Z < 1,64) = 0,95; P(Z < 1,88) = 0,970; P(Z < 2) = 0,977; P(Z < 2,5) = 0,994 Se t tem distribuição de student com 24 graus de liberdade então P(t < 1,71) = 0,95
O tempo, X, que um indivíduo leva para memorizar determinado material é uma variável aleatória normal com média µ minutos e
desvio padrão de 7 minutos. Um psicólogo interessado em estimar µ, selecionou uma amostra de n indivíduos, selecionados ao
acaso, e observou o valor da estatística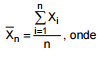 
x = tempo de memorização do i-ésimo indivíduo da amostra.
Desejando-se que o valor observado para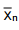 
Desejando-se que o valor observado para X não difira de n µ por mais de 1 minuto com probabilidade de 0,954, o valor de n deverá ser deverá ser
Atenção: Considere as informações a seguir para responder às questões de números 86 a 88.
A distribuição dos salários dos 1000 funcionários da companhia A, em número de salários mínimos, está apresentada na tabela
abaixo: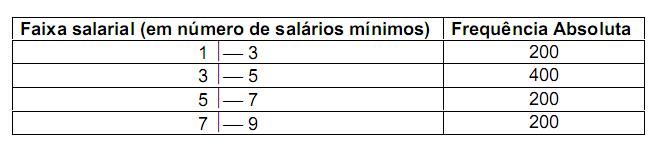 
O valor de X-md, em número de salários mínimos, é 
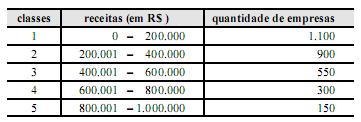
Com base nos dados do quadro acima, em que se demonstra a
distribuição de frequência das receitas de todas as empresas de uma
cidade, julgue os itens a seguir.
A frequência acumulada relativa das empresas que estão nas classes de 1 a 3 é de 85%.
Os preços em reais (R$) para uma amostra de equipamentos de som estão indicados na tabela abaixo. 
Com base na amostra, o valor CORRETO da mediana é igual a:
Atenção: Para resolver as questões de números 55 a 57, dentre informações dadas abaixo, utilize aquelas que julgar apropriadas.
Se Z tem distribuição normal padrão, então:
P(Z<0,5) = 0,691; P(Z < 1) = 0,841; P(Z<1,5) = 0,933; P(Z<2) = 0,977; P(Z<2,58) = 0,995.
Na fabricação de certa peça utilizada em aeronaves usa-se um tipo de elemento cujo diâmetro, X, é uma variável N (2,5 cm; 0,04 cm2). A fábrica que produz tal elemento tem, sobre a venda deste, um lucro dado pela variável L. Sabe-se que L assume os seguintes valores:
L = 100 reais, se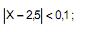
L = 50 reais, se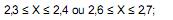
L = - 10 reais se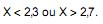 
O lucro médio de um elemento dessa produção, em reais, é igual a
Seja a variável aleatória bidimensional (X,Y) com função de probabilidade dada por: 
A variância da variável aleatória Z = X + Y é dada por
Atenção: Para resolver as questões de números 44 e 45, considere o modelo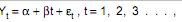 
para prever a quantidade de passagens aéreas emitidas
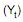em uma região, em milhões de unidades, no ano (2002+t). a e ß são parâmetros desconhecidos e et corresponde ao erro aleatório com as respectivas hipóteses da regressão linear simples.Para a obtenção das estimativas de a e ß, utilizou-se o método dos mínimos quadrados, considerando as observações de
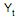de 2003 a 2010.
Com base na equação da reta, obtida pelo método dos mínimos quadrados, obtém-se que, para 2011, a previsão da quantidade de passagens emitidas, em milhões de unidades, é igual a
