Em uma distribuição de valores determinando uma curva de frequência unimodal, verificou-se que o valor da mediana é superior ao valor da moda e inferior ao valor da média. Considere as seguintes informações:
I. A curva possui a cauda mais alongada à direita.
II. A distribuição é assimétrica à direita.
III. A amplitude do intervalo entre a moda e a mediana é inferior à amplitude do intervalo entre a mediana e a média.
IV. Os valores da distribuição estão fortemente concentrados em torno da mediana.
V. Metade dos valores da distribuição situam-se entre o valor da moda e o valor da média.
O número de assertivas corretas é igual a
Em uma urna, são colocadas 2 bolas brancas e 4 pretas. Alberto e Beatriz retiram bolas da urna alternadamente, iniciando-se com Alberto, até que a urna esteja vazia. A probabilidade de que a primeira bola branca saia para Alberto é
Ao utilizar um modelo de regressão linear para a avaliação de um imóvel urbano, um engenheiro de avaliações obteve uma equação cujo coeficiente de correlação equivale a 0,9. Os valores de p (p-valor) para a estatística t de cada variável são superiores a 0,05, valor adotado para o nível de confiabilidade do teste t. Supondo-se que a equação obtida tenha atendido aos pressupostos básicos e aos demais critérios de análise e testes de significância, pode-se afirmar que o poder de explicação do modelo equivale a
Atenção: Para resolver as questões de números 55 a 57, dentre informações dadas abaixo, utilize aquelas que julgar apropriadas.
Se Z tem distribuição normal padrão, então:
P(Z<0,5) = 0,691; P(Z < 1) = 0,841; P(Z<1,5) = 0,933; P(Z<2) = 0,977; P(Z<2,58) = 0,995.
Uma metalúrgica produz blocos cilíndricos cujo diâmetro é uma variável aleatória X, com distribuição normal, média µ = 60 mm e desvio padrão σ = 9 mm. Os diâmetros de uma amostra de 9 blocos são medidos a cada hora, e a média da amostra é usada para decidir se o processo de fabricação está dentro dos padrões de qualidade exigidos. A regra de decisão envolvida no procedimento de qualidade é a seguinte:
Se o diâmetro médio da amostra de 9 cilindros for superior a 64,5 mm ou inferior a 54 mm, o processo deve ser interrompido para ajustes; caso contrário o processo de fabricação continua.
A probabilidade do processo parar desnecessariamente (isto é, parar quando a média µ e o desvio padrão s permanecem sendo os valores acima citados) é de
Atenção: Para resolver às questões de números 52 e 53, considere os dados abaixo:
A empresa de aviação T tem 4 balcões de atendimento ao público: A, B, C e D. Sabe-se que, num determinado dia, os balcões A e B atenderam, cada um, a 20%; C e D atenderam, cada um, a 30% do público que procurou atendimento em T. Sabe-se ainda que A, B, C e D atenderam, respectivamente, 5%, 15%, 10% e 20% de pessoas com atendimento prioritário (idosos, deficientes, gestantes ou mães com crianças no colo, etc).
Selecionando-se ao acaso uma pessoa atendida por T, nesse mesmo dia, a probabilidade dela ter sido atendida no balcão C, sabendo-se que era do grupo de atendimento prioritário, é igual a
Seja a variável aleatória contínua X com função densidade de probabilidade dada por: 
Nessas condições, o valor de K deve ser
Atenção: Para resolver as questões de números 44 e 45, considere o modelo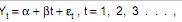 
para prever a quantidade de passagens aéreas emitidas
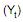em uma região, em milhões de unidades, no ano (2002+t). a e ß são parâmetros desconhecidos e et corresponde ao erro aleatório com as respectivas hipóteses da regressão linear simples.Para a obtenção das estimativas de a e ß, utilizou-se o método dos mínimos quadrados, considerando as observações de
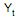de 2003 a 2010.
Considerando o quadro de análise de variância, é correto afirmar que
Seja uma população da qual se extrai uma amostra aleatória grande de tamanho n. Com relação à aplicação do método de reamostragem bootstrap, é correto afirmar que tal método
Duas empresas X e Y possuem 150 e 100 empregados, respectivamente. A média aritmética dos salários da empresa X supera a da empresa Y em R$ 500,00 e o desvio padrão da empresa X supera o da empresa Y em R$ 200,00. Se os coeficientes de variação das empresas X e Y são respectivamente iguais a 20% e 15%, então a média aritmética de todos os empregados das empresas X e Y, em conjunto, apresenta o valor de
A tabela de frequências relativas abaixo corresponde à distribuição da renda mensal das pessoas que adquiriram pacotes de excursão de uma empresa de turismo em 2010. O valor da média aritmética da renda (Me) foi obtido considerando que todos os valores incluídos num certo intervalo de classe são coincidentes com o ponto médio deste intervalo. O valor da mediana (Md) foi obtido pelo método da interpolação linear.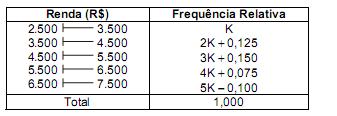 
O valor da moda (Mo), obtido pela relação de Pearson: Mo = 3Md - 2Me , é igual a
A distribuição de frequências de uma certa amostra é representada no gráfico abaixo.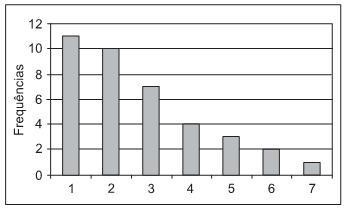
Sobre a média µ, a mediana m e a moda M dessa amostra, tem-se
Julgue os seguintes itens, considerando que a distribuição conjunta
de duas variáveis aleatórias contínuas X e Y seja dada pela
expressão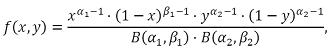 
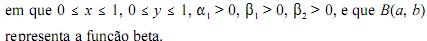
A covariância entre X e Y é nula.
Considere a distribuição conjunta de duas variáveis aleatórias
discretas X e Y dada pela expressão seguinte: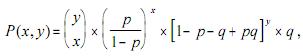
em que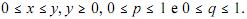 
Julgue os seguintes itens a respeito dessa distribuição.
As distribuições marginais X/Y = y e Y são, respectivamente, binomial (y, p) e geométrica (q).
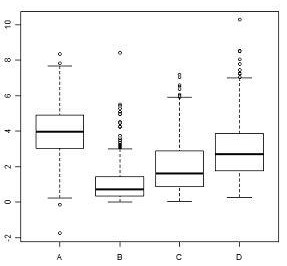
Considerando o gráfico acima e o fato de os pontos indicarem uma
única observação, julgue os itens que se seguem, referentes ao
coeficiente de assimetria.
Entre os grupos B, C e D, o que tem o menor coeficiente de assimetria é o grupo D.
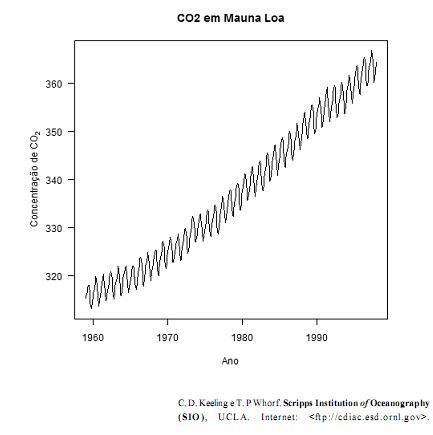
A partir da figura acima, que ilustra a evolução temporal
(de janeiro/1959 a dezembro/1997) dos níveis mensais de
concentração de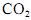 
registrados em determinada localidade, julgue
os itens de 40 a 42.
Considere a seguinte situação hipotética.
Um pesquisador resolveu extrair a tendência da série temporal Y ( t ) sem a componente sazonal, por meio de uma regressão linear simples na forma Y ( t ) = a + bt +e ( t ), em que t = 0 corresponde a jan/59, t = 1 corresponde a fev/59, ..., e t = 468 corresponde a dez/97. Esse pesquisador tomou como série livre de tendências a série dos resíduos, em que Y(t) é a série ajustada pelo modelo de regressão. As séries y( t ) e Y ( t - Y (t) são mostradas nos gráficos abaixo.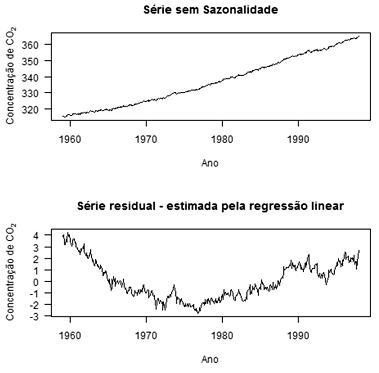
Com base nessas informações, é correto afirmar que a regressão linear simples foi um processo eficaz para extrair a tendência da série temporal em questão.
