Após o lançamento de um novo modelo de automóvel observou-se que 20% deles apresentavam defeitos na suspensão, 15% no sistema elétrico e 5% na suspensão e no sistema elétrico. Selecionaram-se aleatoriamente e com reposição 3 automóveis do modelo novo. A probabilidade de pelo menos dois apresentarem algum tipo de defeito é
Relativamente à Análise de Séries Temporais, considere as afirmativas abaixo.
I. O teste de Box- Pierce é um teste baseado nas autocorrelações dos resíduos estimados e serve para diagnosticar se o modelo ajustado à série é adequado.
II. Um modelo ARIMA(1,0,1) é estacionário se o coeficiente autoregressivo for um número, em módulo, maior do que um.
III. O modelo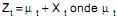 
é uma função determinística periódica, satisfazendo 
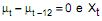é um processo estacionário que pode ser modelado por um ARMA (p, q), exibe um comportamento sazonal estocástico.
IV. Um modelo AR (1) tem função de autocorrelação parcial com decaimento exponencial dominante.
Está correto o que se afirma APENAS em:
Seja X uma variável aleatória contínua com função densidade de probabilidade dada por: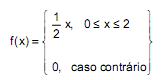 
Se F(x) é a função de distribuição acumulada de X, então
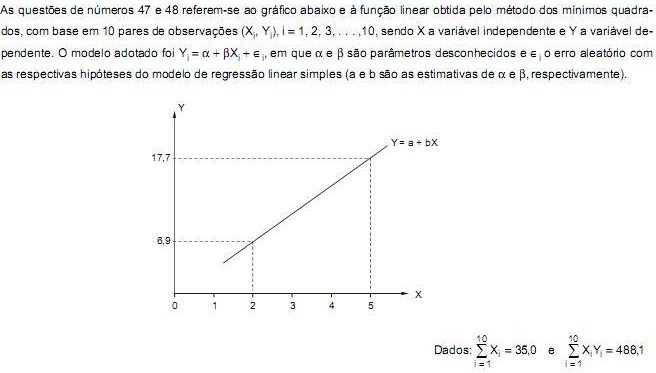
A variação explicada pelo modelo de regressão apresenta o valor de
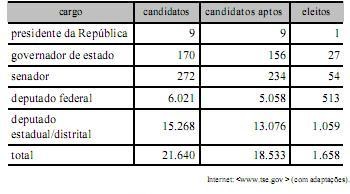
Com base na tabela acima, referente às eleições de 2010, que apresenta a quantidade de candidatos para os cargos de presidente da República, governador de estado, senador, deputado federal e deputado estadual/distrital, bem como a quantidade de candidatos considerados aptos pela justiça eleitoral e o total de eleitos para cada cargo pretendido, julgue os itens a seguir.
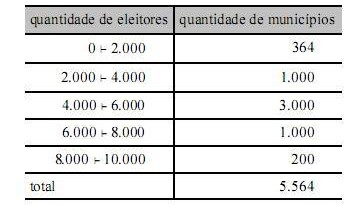
A tabela acima apresenta uma distribuição hipotética das quantidades de eleitores que não votaram no segundo turno da eleição para presidente da República bem como os números de municípios em que essas quantidades ocorreram. Com base nessa tabela, julgue os itens segunites, relativos à análise exploratória de dados.
A curtose da distribuição em questão pode ser avaliada com base na estimativa do quarto momento central, a qual deve ser comparada com o valor de referência 3, visto que todas as distribuições simétricas possuem quarto momento central igual a 3.
Julgue os itens que se seguem, referentes às técnicas de amostragem e de inferência estatística.
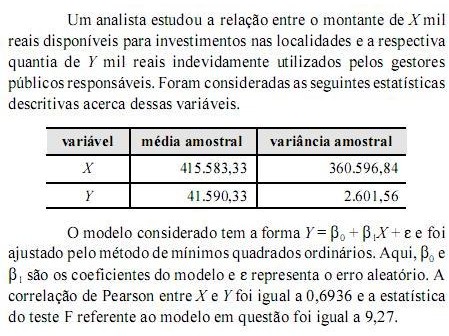
Com base nessas informações, julgue os próximos itens, relativos a correlação, regressão e distribuições conjuntas.
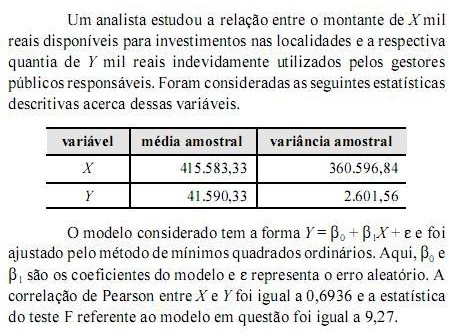
Com base nessas informações, julgue os próximos itens, relativos a correlação, regressão e distribuições conjuntas.
Caso o analista deseje aumentar o tamanho da amostra, mas alguns valores dos recursos desviados estejam censurados, então, o modelo a ser utilizado é o modelo PROBIT.
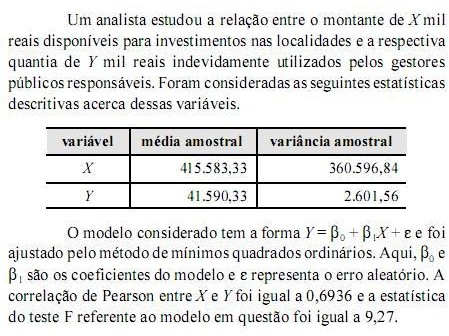
Com base nessas informações, julgue os próximos itens, relativos a correlação, regressão e distribuições conjuntas.
Com relação ao algoritmo EM (expectation-maximization), julgue os itens que se seguem.
Se o logaritmo da função de verossimilhança do par de variáveis aleatórias (Z, W) for proporcional ao logaritmo da função de verossimilhança de outro par de variáveis aleatórias (X, Y), ou seja, l(2, Z, W) = h(2) l(2; X, Y) , em que, h(2) < 0, então a estimativa de máxima verossimilhança para o parâmetro 2 obtida com o algoritmo EM será idêntica para quaisquer desses pares de variáveis aleatórias.
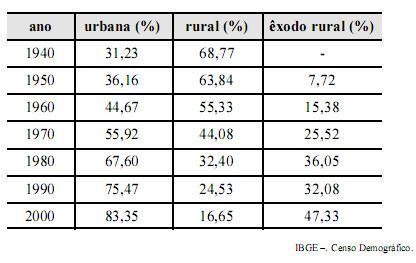
A tabela acima apresenta a distribuição percentual da população brasileira em área rural e urbana, nos períodos de 1940 a 2000. A coluna êxodo rural mostra o percentual das pessoas que migraram do campo para a área urbana. Com base nessas informações, julgue os itens subsequentes.
Supondo que, em cada década, a taxa de êxodo rural seja linear, é correto estimar que em 1966 a população urbana no Brasil tinha o mesmo tamanho da população rural.
Considere que os valores abaixo representem as massas (em kg) de 10 unidades de determinado produto selecionadas aleatoriamente em uma linha de produção, em determinado momento: 7,56; 7,64; 5,81; 10,80; 10,07; 7,85; 9,29; 10,34; 10,16; 10,95. Considere também que os valores aproximados da média amostral e do desvio padrão desses valores sejam, respectivamente, 9,05 kg e 1,64 kg. Em face dessas informações, julgue os próximos itens, acerca de controle estatístico de qualidade.
