Considerando um vetor aleatório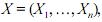 
julgue o item que se segue.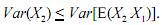
Julgue os itens que se seguem, relativos a curtose.
A distribuição será leptocúrtica se o coeficiente de excesso de curtose for negativo.
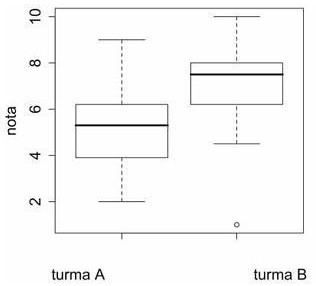
Com base na figura acima, que apresenta uma comparação entre as
notas finais obtidas pelos alunos das turmas A e B de determinada
disciplina, julgue os itens a seguir.
A nota mínima na turma A é menor que a nota mínima na turma B.
Em um estudo clínico utilizou-se um modelo de regressão logística
em que y é a variável resposta, como preditor linear, a expressão
a + bx + cz, em que x = 0 para o grupo placebo e x = 1 para o grupo
de tratamento; z é uma medida de colesterol (em escala de 0 a 5)
antes do início do tratamento. Com base nessas informações, julgue
os itens subsequentes
A variável resposta y é binária.
A partir do modelo linear clássico em forma matricial y = Xb +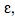 
denotando-se por e = y -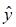 
o vetor de resíduos do modelo
estimado por mínimos quadrados ordinários, julgue os seguintes
itens.
A hipótese nula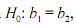 
em que 
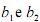são os elementos do vetor b, pode ser avaliada pelo teste F. Nesse teste, a soma de quadrados de resíduos do modelo completo é comparada com a soma de quadrados de resíduos do modelo restrito sob a hipótese nula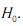 
Julgue, em cada um dos itens seguintes, se está correta a associação
entre método numérico e procedimento estatístico.
decomposição de Choleski 
integração numérica de função densidade
Com relação a indicadores demográficos, julgue os itens a seguir.
Fecundidade representa o potencial reprodutivo; fertilidade representa o resultado efetivo do potencial reprodutivo.
Julgue o próximo item, referente a determinado método computacionalmente intensivo.
O bootstrap consiste em um procedimento de reamostragem que se baseia na geração de repetições das observações sem reposição.
Considerando-se duas variáveis aleatórias contínuas X e Y, em que
X tem função de densidade arbitrária f com função geradora de
momentos M(t) e Y = exp(X), julgue os próximos itens.
E(Y) = exp[E(X)].
Considerando que X, Y e Z sejam variáveis aleatórias, que a seja
uma constante não nula e que E, Md, Var, Cov,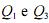 
denotem,
respectivamente, esperança, mediana, variância, covariância,
primeiro quartil e terceiro quartil, julgue os itens a seguir.
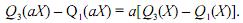
Considerando que X, Y e Z sejam variáveis aleatórias, que a seja
uma constante não nula e que E, Md, Var, Cov,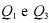 
denotem,
respectivamente, esperança, mediana, variância, covariância,
primeiro quartil e terceiro quartil, julgue os itens a seguir.
Var(X Y) = Var(X) Var(Y) + 2Cov(X Y).
Considere que os salários de todos os 530 empregados de uma empresa sejam normalmente distribuídos com uma média µ e um desvio padrão populacional igual a R$ 149,50. Uma amostra aleatória de 169 destes salários (sem reposição) apresentou uma média de X reais. Com base no resultado da amostra, deseja-se testar a hipótese, ao nível de significância de 5%, se µ é superior a R$ 2.000,00 sendo formuladas as hipóteses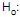 
µ = R$ 2.000,00 (hipótese nula) e 
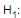µ > R$ 2.000,00 (hipótese alternativa). Sabe-se que 
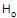não foi rejeitada considerando a informação da distribuição normal padrão (Z) que a probabilidade P (z > 1,64) = 0,05. O valor de X é, no máximo,
Uma população normal e de tamanho infinito apresenta uma média µ e variância populacional igual a 0,81. Pretende-se obter, a partir de uma amostra aleatória de tamanho 144 dessa população, um intervalo de confiança de 95% para µ. Considerando na distribuição normal padrão (Z) as probabilidades P(z > 1,96) = 0,025 e P(z > 1,64) = 0,05, o intervalo apresenta uma amplitude de
A soma dos valores de todos os 50 elementos de uma população X é igual a 2.750. O coeficiente de variação para esta população apresenta o valor de 20%. Então, o valor da soma dos quadrados de todos os elementos de X é
As questões de números 64 a 67 referem-se em informações dadas abaixo.
Se Z tem distribuição normal padrão, então:
P (Z < 0,28) = 0,61; P (Z < 1,28) = 0,9; P (Z < 1,5) = 0,933; P (Z < 1,96) = 0,975; P (Z < 2) = 0,977.
O valor de n para que a diferença, em valor absoluto, entre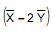 
e sua média seja inferior a 3, com probabilidade de 86,6%, é
