Julgue os seguintes itens, considerando que a distribuição conjunta
de duas variáveis aleatórias contínuas X e Y seja dada pela
expressão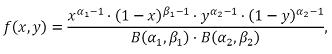 
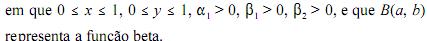
Se a distribuição estiver definida dentro do quadrado [0,1] × [0,1], então a probabilidade de uma realização (x, y) estar dentro do círculo de centro (½, ½) e raio ½ será igual a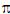 
/4.
Julgue os itens que se seguem, acerca de análise exploratória de
dados, análise de dados discretos, análise de regressão e inferência
estatística.
Considere duas variáveis X e Y com correlação linear de Pearson igual a 0,75. Nesse caso, somente se a variância de Y for superior ao dobro da variância de X, a variável Y tenderá a crescer pelo menos 1,5 unidades para cada unidade que aumentar a variável X .
Considerando que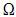 
seja uma matriz de variância-covariância de
ordem p , julgue os itens que se seguem.
Julgue os itens que se seguem, a respeito de análise de dados
discretos.
Em uma amostra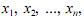 
em que 
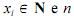é ímpar, a mediana é um número inteiro.
Com relação a processos de Markov com matriz de
transição M =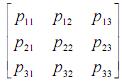 
, em que 
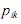representa
probabilidade de transição do estado i para o estado k , julgue os
seguintes itens.
Um processo de Markov irredutível, aperiódico e ergódico não possui distribuição estacionária.
Considerando que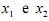 
sejam variáveis contínuas, julgue os
próximos itens a respeito do seguinte problema de programação
linear: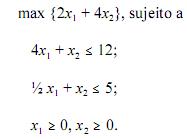
No problema dual, o ponto (2, 1) não é viável.
No que concerne aos planos amostrais, julgue os itens a seguir.
Tanto na amostragem estratificada quanto na amostragem por conglomerados, a população é dividida em grupos. Na amostragem por conglomerados, de cada grupo seleciona-se um conjunto de elementos; na amostragem estratificada, devem-se selecionar quais estratos serão amostrados e, desses, observar todos os elementos.
Com o propósito de estimar o valor do número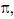 
um estudante
efetuará o seguinte experimento computacional:
1. gerará uma amostra aleatória simples de n coordenadas,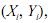 
i = 1,
, n, em que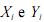 
são independentes e têm distribuição
uniforme contínua no intervalo (0, L), L > 0;
2. contará o número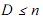 
desses pontos que estão no interior da
circunferência de raio r = L/2 e centro no ponto (L/2, L/2).
Em relação ao experimento descrito, julgue os itens subsequentes.
O experimento descrito para estimação do número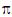 
é exemplo de aplicação do método de Monte Carlo.
Com relação aos testes de hipóteses paramétricos, julgue os itens
subsecutivos.
Define-se poder do teste como a probabilidade de a hipótese nula ser rejeitada quando esta é, de fato, falsa. Logo, o poder do teste é igual a 1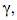 
em que 
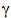é a probabilidade de haver o erro do tipo I.
Considerando que X seja uma variável aleatória cuja função de
probabilidade acumulada, F(x), é expressa por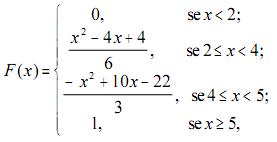
julgue os seguintes itens.
função F(x) é contínua e diferenciável em todo o seu domínio.
Desejando-se estimar a proporção p de pessoas favoráveis a certo projeto governamental numa população, utilizou-se a proporção amostral p , com base numa amostra aleatória simples, com reposição de 200 observações. Se temos a informação que 0 = p = 0,4, e se var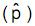 
representa a variância de 
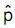, então
Considere as afirmativas abaixo.
I. A taxa de mortalidade infantil é definida como o número de mortes durante um ano-calendário entre os bebês com menos de um ano de idade dividido pelo número total de nascidos vivos durante aquele ano.
II. O sexo e a raça dos indivíduos em uma população não têm efeito significativo nas taxas que descrevem as estatísticas vitais.
III. Dados demográficos lidam exclusivamente com o crescimento de uma população.
Está correto o que se afirma APENAS em
Um estudo apresentou em seu relatório um problema de programação linear que é descrito abaixo.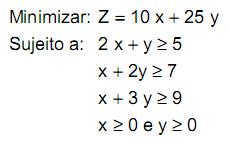 
Os valores de x e y são, respectivamente,
A média aritmética dos salários de todos os empregados de uma empresa é igual a R$ 2.000,00 com um coeficiente de variação igual a 10%. A partir de uma certa data é concedido um reajuste de 10% e um adicional fixo de R$ 300,00 para estes salários.
Então, é correto afirmar que
