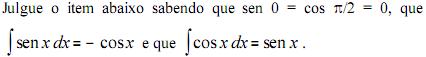Se a função densidade de probabilidade da variável aleatória bidimensional contínua (X, Y) é dada por: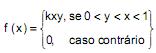
O valor de k é
Considere a variável aleatória contínua X com função densidade de probabilidade dada por: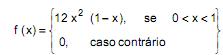 
Se Mo (X) representa a moda de X, então P [X = Mo (X)] é igual a
As questões de números 56 e 57 referem-se as informações dadas abaixo.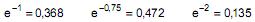 
Sabe-se que 2% dos itens produzidos na fábrica A são defeituosos. Selecionando-se ao acaso e com reposição uma amostra de 100 itens da produção de A, a probabilidade de pelo menos 2 serem defeituosos, probabilidade esta calculada usando a aproximação pela distribuição de Poisson, é
Sejam A e B dois eventos de um mesmo espaço amostral. Sabe-se que: P (A) = 0,4 e P (B) = 0,75. Nessas condições, é verdade que:
Em um modelo de regressão linear múltipla envolvendo a variável dependente e 4 variáveis explicativas, obtiveram-se as estimativas dos respectivos parâmetros utilizando o método dos mínimos quadrados. O número de observações para a dedução da correspondente equação foi de 20. Construindo o quadro de análise de variância, com o objetivo de testar a existência da regressão, tem-se para utilização da estatística F de Snedecor os graus de liberdade no numerador e no denominador com, respectivamente,
Seja uma variável aleatória X, em que uma amostra aleatória de 6 elementos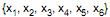 
com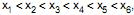
, foi extraída da população. Considerando que 
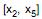é um intervalo de confiança para a mediana de X, o nível de confiança deste intervalo é
Com relação a bioestatística, um ramo da estatística aplicado às
ciências biológicas e à área de saúde, julgue os itens que se seguem.
Uma amostragem é considerada não probabilística quando é usada alguma forma de sorteio para a obtenção da amostra.
Sabe-se que (X,Y) é uma variável aleatória bidimensional com função densidade de probabilidade dada por: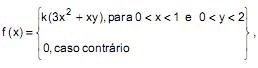
onde k é um parâmetro real.
Nessas condições, a distribuição marginal de X, para 0 < x < 1, é
Um experimento pode resultar em sucesso ou fracasso com probabilidades 0,25 e 0,75, respectivamente. Considere a variável aleatória X= número de fracassos antes de ocorrer o primeiro sucesso. A probabilidade de X ser pelo menos 2 e a média de X são dadas, respectivamente, por
Um analista de mercados está coletando informações sobre a variável X = preço de determinado produto. Ele coletou uma amostra aleatória, sem reposição, de tamanho n de uma população de 45 compradores do produto. Sabendo-se que a variância da média amostral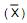 
dos preços pagos pelos n clientes pelo produto é 1/11 da variância populacional (variância de X para a população finita de 45 compradores), o valor de n é
Em uma empresa, a quantidade de empregados de uma categoria profissional é igual a 64. Todos eles são submetidos a uma prova e é anotada a nota de cada empregado. Visando melhorar o desempenho destes profissionais, a empresa promove um treinamento para todos eles durante 6 meses. Posteriormente, uma nova prova é aplicada e verifica-se que 41 deles apresentaram melhora e os restantes foram melhores na primeira prova. Utilizou-se o teste dos sinais para decidir se o treinamento funcionou, a um nível de significância de 5%, considerando que ocorreram 41 sinais positivos para os que apresentaram melhora e 23 negativos para os restantes. Sejam as hipóteses H0: p = 0,50 (hipótese nula) e H1: p > 0,50 (hipótese alternativa), em que p é a proporção populacional de sinais positivos. Aproximando a distribuição binomial pela normal, obteve-se o escore reduzido r (sem a correção de continuidade), para ser comparado com o valor crítico z da distribuição normal padrão (Z) tal que a probabilidade P(Z>z) = 0,05. O valor de r é tal que
Seja X uma variável aleatória normalmente distribuída com média µ e variância populacional desconhecida. Deseja-se testar a hipótese em que a média µ da população, considerada de tamanho infinito, é superior a 20, ao nível de significância de 5%. Para testar a hipótese, foi extraída uma amostra aleatória de 9 elementos, apurando-se uma média igual a 21 e com a soma dos quadrados destes elementos igual a 3.987. As hipóteses formuladas foram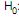 
: µ = 20 (hipótese nula) e 
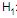: µ > 20 (hipótese alternativa). Utilizando o teste t de Student, obtém-se que o valor da estatística 
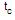(t calculado), para ser comparado com o t tabelado, é igual a
Considere os estimadores não viezados E e E da média µ, dados abaixo, de uma população normal com variância unitária. (X, Y, Z) corresponde a uma amostra aleatória de tamanho 3 da população com m e n sendo parâmetros reais.
E = mX + (m - n)Y + (2m - n)Z
E = mX + (3m - n)Y + mZ
É correto afirmar que
Atenção: Para resolver as questões de números 97 a 99, utilize, dentre informações dadas a seguir, as que julgar apropriadas: Se Z tem distribuição normal padrão, então: P (Z < 1) = 0,841; P (Z < 1,64) = 0,95; P (Z < 1,88) = 0,970; P (Z < 2) = 0,977; P (Z < 2,5) = 0,994
O tempo X que um indivíduo leva para memorizar determinado material é uma variável aleatória normal com média µ minutos
e desvio padrão de 7 minutos. Um psicólogo, interessado em estimar µ, selecionou uma amostra de n indivíduos, ao acaso, e
observou o valor da estatística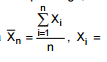 
tempo de memorização do i-ésimo indivíduo da amostra.
Desejando-se que o valor observado para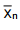 
não difira de n µ por mais de 1 minuto com probabilidade de 0,954, o valor de n
deverá ser
