Julgue os itens que se seguem, acerca de análise exploratória de
dados, análise de dados discretos, análise de regressão e inferência
estatística.
Suponha que uma variável, que segue uma distribuição normal, tenha sido observada em uma amostra composta pelos grupos A e B, e que os diagramas abaixo mostrem os esquemas dos cinco números de cada um desses grupos.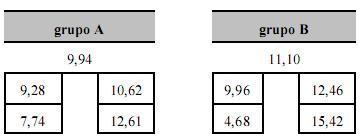
Considerando-se essas informações, e que os tamanhos amostrais sejam iguais a 100 unidades, é correto afirmar que um teste de comparações de médias aponta diferenças estatisticamente significativas entre as médias dos dois grupos.
Considerando que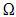 
seja uma matriz de variância-covariância de
ordem p , julgue os itens que se seguem.
Com relação a processos de Markov com matriz de
transição M =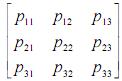 
, em que 
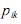representa
probabilidade de transição do estado i para o estado k , julgue os
seguintes itens.
Se M = 
, então o processo de Markov definido por essa matriz de transição é tempo-reversível.
Considerando que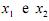 
sejam variáveis contínuas, julgue os
próximos itens a respeito do seguinte problema de programação
linear: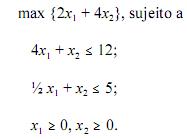
Esse problema possui infinitas soluções ótimas.
Considerando que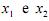 
sejam variáveis contínuas, julgue os
próximos itens a respeito do seguinte problema de programação
linear: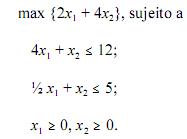
Se x for uma solução primal viável e se for uma solução dual viável, então f(x)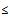 
g(y), em que é a função objetivo primal e g é a função objetivo dual.
Considere o modelo de regressão linear simples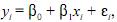 
em que i = 1, 2,
, n; y represente a variável resposta; x seja a
variável independente;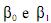 
sejam constantes; e as variáveis
aleatórias 
sejam independentes e normais com média zero
e variância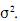 
Acerca desse modelo, julgue os seguintes itens.
Se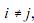 
então 
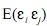= 0.
Com o propósito de estimar o valor do número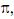 
um estudante
efetuará o seguinte experimento computacional:
1. gerará uma amostra aleatória simples de n coordenadas,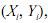 
i = 1,
, n, em que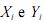 
são independentes e têm distribuição
uniforme contínua no intervalo (0, L), L > 0;
2. contará o número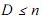 
desses pontos que estão no interior da
circunferência de raio r = L/2 e centro no ponto (L/2, L/2).
Em relação ao experimento descrito, julgue os itens subsequentes.
O número D segue uma distribuição binomial.
Com relação aos testes de hipóteses paramétricos, julgue os itens
subsecutivos.
A análise de variância (ANOVA), que é generalização do teste t , permite testar se as variâncias de vários grupos diferentes são ou não iguais.
Considerando que X seja uma variável aleatória cuja função de
probabilidade acumulada, F(x), é expressa por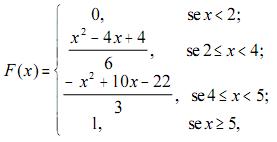
julgue os seguintes itens.
Estão em uma sala quatro pessoas que foram convocadas
por um juiz: duas delas efetivamente testemunharão; as outras se
recusarão a testemunhar acerca de determinado fato. O juiz chamará
essas pessoas, uma a uma, para outra sala, mediante sorteio
aleatório. Considere que X seja a variável aleatória que indica o
número de pessoas chamadas até se encontrar a primeira pessoa
disposta a testemunhar.
Com base nessa situação hipotética, julgue os itens que se seguem.
A probabilidade de X ser igual a 1 ou 2 é superior a 0,8.
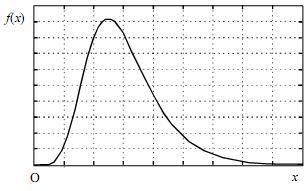
Considerando a figura acima, que ilustra a função de densidade de
probabilidade de uma variável aleatória X, julgue o seguinte item.
Infere-se do gráfico acima que a distribuição é assimétrica à direita e, portanto, o valor médio de X é maior que a sua mediana.
O gerente de produção de uma indústria de um determinado tipo de peça deseja testar a hipótese, ao nível de significância de 5%, de que a variância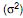 
dos comprimentos das peças fabricadas é inferior a 10 cm2. As hipóteses formuladas foram 
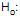s2 = 10 cm2 (hipótese nula) e 
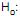s2 < 10 cm2 (hipótese alternativa). Tirou-se uma amostra aleatória de apenas 18 peças obtendo-se uma variância igual a 9 cm2 para esta amostra. Foi utilizado o teste do qui-quadrado com as seguintes informações da correspondente distribuição para o nível de significância de 5%: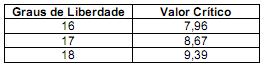 
Com base no resultado da amostra e supondo que a distribuição da população dos comprimentos das peças é normal e de tamanho infinito, é correto afirmar:
Uma amostra aleatória de 9 elementos foi extraída de uma população normal de tamanho infinito com média µ e variância desconhecida. O desvio padrão da amostra apresentou o valor de 1,25 e o intervalo de confiança de (1 - a) para µ: [14, 16] fo obtido com base nesta amostra. Sabe-se que para obtenção deste intervalo utilizou-se a distribuição t de Student com os correspondentes graus de liberdade, em que a probabilidade P (- T= t = T) = (1 - a). Se T > 0, então o valor de T é
Utilizando o Teorema de Tchebyshev, obteve-se que o valor máximo da probabilidade dos empregados de uma empresa, que ganham um salário igual ou inferior a R$ 1.500,00 ou um salário igual ou maior a R$ 1.700,00, é 25%. Sabendo-se que a média destes salários é igual a R$ 1.600,00, encontra-se a respectiva variância, em (R$) 2, que é
Em dezembro de 2010, a distribuição dos valores dos salários recebidos pelos empregados de uma empresa é apresentada pela tabela de frequências relativas abaixo, em que todos os intervalos de classe têm a mesma amplitude.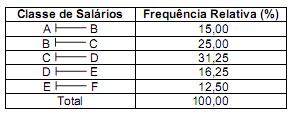 
Sabe-se que C = R$ 2.500,00 e que o valor da mediana, obtido por interpolação linear, é igual a R$ 2.820,00. Então, utilizando interpolação linear, obtém-se o valor do primeiro quartil da distribuição que é igual a
