Um histograma representa a distribuição dos preços unitários de venda de um determinado equipamento no mercado. No eixo das ordenadas estão assinaladas as respectivas densidades de frequência para cada intervalo em (R$) -1. Define-se densidade de frequência de um intervalo de classe como sendo o quociente da divisão da respectiva frequência relativa pela correspondente amplitude do intervalo. Um intervalo de classe do histograma corresponde aos preços unitários maiores ou iguais a R$ 32,00 e inferiores a R$ 44,50 com uma densidade de frequência igual a 1,6 × 10-2 (R$) -1. Se todos os intervalos de classe do histograma têm a mesma frequência relativa, então um intervalo de classe com densidade de frequência igual a 5,0 × 10-3 (R$) -1 apresenta uma amplitude de
Relativamente à Análise Multivariada de Dados, considere as afirmativas abaixo.
I. A análise fatorial é um exemplo de técnica de interdependência, o que significa que nenhuma variável ou grupo de variáveis é definida como sendo dependente ou independente.
II. A análise de correlação canônica não é adequada se as variáveis independentes são quantitativas.
III. A análise discriminante múltipla é adequada se a única variável dependente for categórica.
IV. A análise de correspondência não é adequada para teste de hipóteses.
Está correto o que se afirma APENAS em
As questões de números 64 a 67 referem-se em informações dadas abaixo.
Se Z tem distribuição normal padrão, então:
P (Z < 0,28) = 0,61; P (Z < 1,28) = 0,9; P (Z < 1,5) = 0,933; P (Z < 1,96) = 0,975; P (Z < 2) = 0,977.
O peso de um produto é uma variável aleatória X que tem distribuição normal com média µ e desvio padrão s. Sabendo-se que 80% dos valores de X estão entre (µ - 12,8) gramas e (µ + 12,8) gramas e que 39% são maiores do que 600 gramas, os valores de µ e s , em gramas, são dados, respectivamente, por
As questões de números 56 e 57 referem-se as informações dadas abaixo.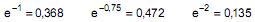 
O tempo de espera, em minutos, para a utilização de um caixa eletrônico 24 horas por clientes de certos bancos, num determinado aeroporto, é uma variável aleatória exponencial com média de 4 minutos. A probabilidade de um cliente esperar até 3 minutos para utilizar esse caixa é
Foram obtidas n observações independentes de uma variável aleatória X com distribuição uniforme contínua no intervalo [0, 1]. Sabe-se que a probabilidade de exatamente uma dessas observações ser menor do qu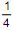e 
é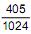 
. Nessas condições, o valor de n é
Um estudo corresponde ao interesse de analisar o desempenho de 3 postos independentes de atendimento ao público com 8 funcionários cada um. Decidiu-se empregar a análise de variância com o objetivo de testar a hipótese de igualdade das médias de atendimento dos 3 postos (quantidade de pessoas atendidas por mês). Durante um mês, anotou-se para cada funcionário dos postos a quantidade de pessoas atendidas. Denominando os postos por Grupo 1, Grupo 2 e Grupo 3 obteve-se pelo quadro de análise de variância o valor da estatística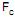 
(F calculado) igual a 2, para posteriormente comparar com o F tabelado (variável F de Snedecor). A porcentagem que a variação entre os grupos representa da variação total no quadro de análise de variância é igual a
Três marcas (X, Y e Z) de um equipamento foram testadas, a um determinado nível de significância, para determinar se havia diferença entre suas vidas médias em horas. Utilizou-se o teste de Kruskal-Wallis com base em três amostras aleatórias, uma de cada marca, sendo 6 equipamentos de X, 8 equipamentos de Y e 10 equipamentos de Z. As observações das vidas dos 24 equipamentos foram dispostas em ordem crescente sendo atribuídos postos para as respectivas vidas. Posteriormente, calculou-se o valor da estatística H utilizado para comparação com o qui-quadrado tabelado. É correto afirmar que
A função de produção de uma determinada empresa é representada pelo expressão Q = A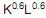 
, onde Q é a produção, K e L são os fatores de produção, e A é um parâmetro com valor fixo.
Sobre essa função de produção, afirma-se que ela apresenta retornos de escala
Ao medir-se a temperatura de um forno, em graus Celsius, em diversos momentos, obteve-se uma amostra com variância igual a 225. Se cada uma das medidas de temperatura for convertida para graus Fahrenheit, utilizando-se a fórmula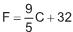 
, o valor da nova variância amostral será
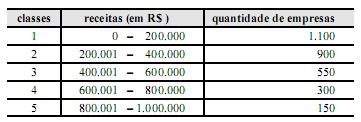
Com base nos dados do quadro acima, em que se demonstra a
distribuição de frequência das receitas de todas as empresas de uma
cidade, julgue os itens a seguir.
É correto inferir que a média das receitas das empresas da cidade em apreço é inferior a R$ 332 mil.
A quantidade diária de unidades vendidas do produto X em uma determinada indústria segue uma distribuição normal, com média de 1.000 unidades e desvio padrão de 200 unidades. O gráfico abaixo representa a distribuição normal padrão com média igual a 0 (zero) e desvio-padrão igual a 1 (um), cujas percentagens representam as probabilidades entre os valores de desvio-padrão.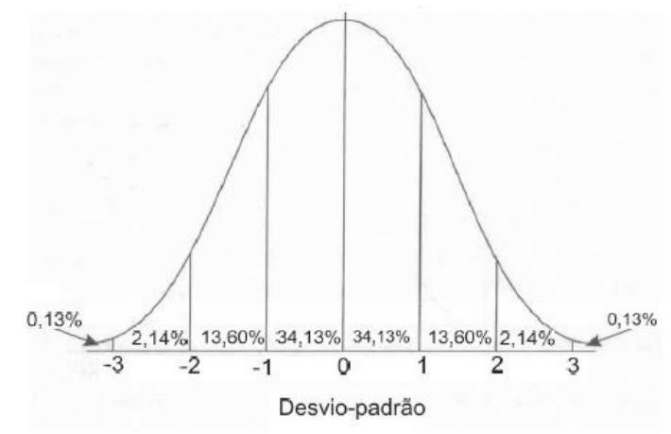 
Com base nas informações fornecidas, é CORRETO afirmar que:
Relativamente à Análise Multivariada de Dados, considere:
I. Na análise discriminante, uma suposição para a determinação da função discriminante é a de normalidade multivariada das variáveis independentes.
II. A análise de correspondência não é sensível a observações atípicas, como outliers.
III. A escalagem multidimensional se baseia em distâncias euclidianas em projeção plana entre variáveis.
É correto o que consta APENAS em
Atenção: Para resolver as questões de números 55 a 57, dentre informações dadas abaixo, utilize aquelas que julgar apropriadas.
Se Z tem distribuição normal padrão, então:
P(Z<0,5) = 0,691; P(Z < 1) = 0,841; P(Z<1,5) = 0,933; P(Z<2) = 0,977; P(Z<2,58) = 0,995.
Sabe-se que o tempo para a ocorrência de defeito em uma peça tem distribuição normal com média de 1200 dias e desvio padrão de 100 dias. O fabricante de tais peças oferece aos seus clientes uma garantia de g dias (ele substitui toda peça que durar g dias ou menos). O valor de g para que apenas 0,5% das peças sejam substituídas é, em dias, igual a
Atenção: Para resolver a questão de número 48, dentre as informações dadas abaixo, utilize aquela que julgar apropriada: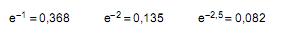 
O número de passageiros que chegam a um posto de atendimento de uma empresa de aviação para fazer o check-in às quartas-feiras pela manhã tem distribuição de Poisson com taxa média de 5 passageiros por minuto. A probabilidade de chegar a esse mesmo posto, numa quarta-feira pela manhã, pelo menos 2 passageiros em 30 segundos, é de
Uma pesquisa é realizada com 285 pessoas de uma região (Região I) e também com 285 pessoas de uma outra região (Região II), independentemente. As pessoas foram escolhidas aleatoriamente e perguntou-se para cada uma qual o tipo de pacote turístico de sua preferência. Cada pessoa deu uma e somente uma resposta entre os pacotes X e Y. O resultado foi o seguinte:
Utilizando o teste qui-quadrado a um nível de significância de 10%, observou-se que o valor crítico da distribuição qui-quadrado com 1 grau de liberdade é inferior ao valor do qui-quadrado observado. O valor do qui-quadrado observado e a conclusão da preferência com relação às regiões, a um nível de significância de 10%, são, respectivamente,
