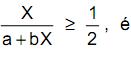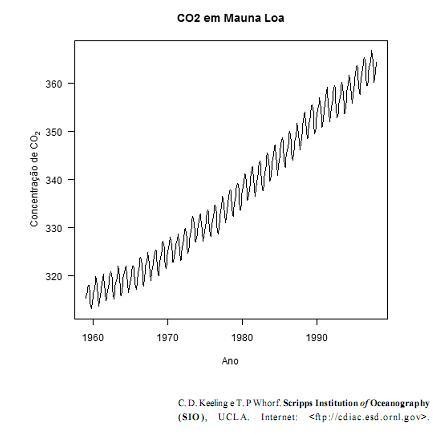
A partir da figura acima, que ilustra a evolução temporal
(de janeiro/1959 a dezembro/1997) dos níveis mensais de
concentração de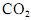 
registrados em determinada localidade, julgue
os itens de 40 a 42.
Suponha que a série sem a componente sazonal tenha sido ajustada por modelos ARIMA, cujos resultados se encontram na tabela abaixo, em que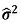 
representa a estimativa da variância do processo, log-veross é o valor do logaritmo da função de verossimilhança e AIC é o critério de informação de Akaike.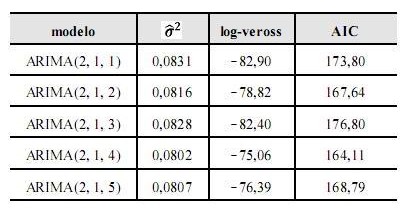
Considerando-se essas informações, é correto afirmar que o modelo sugerido para o ajuste dessa série temporal é o ARIMA(2, 1, 4).
Com relação a processos de Markov com matriz de
transição M =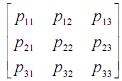 
, em que 
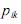representa
probabilidade de transição do estado i para o estado k , julgue os
seguintes itens.
O processo de Markov será irredutível e aperiódico somente se todas as probabilidades de transição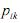 
forem não nulas.
Em relação aos métodos numéricos, julgue os itens que se seguem.
Considere um conjunto de n pontos amostrados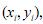 
em que 
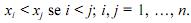Nessa situação, ao contrário do que ocorre na regressão, um modelo f obtido por interpolação deve passar por todos esses pontos amostrados, isto é,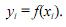 
Considerando que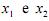 
sejam variáveis contínuas, julgue os
próximos itens a respeito do seguinte problema de programação
linear: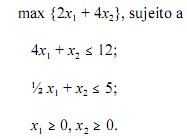
No plano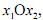 
as curvas de nível da função objetivo formam uma família de retas com coeficiente angular igual a ½.
Considere o modelo de regressão linear simples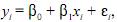 
em que i = 1, 2,
, n; y represente a variável resposta; x seja a
variável independente;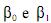 
sejam constantes; e as variáveis
aleatórias 
sejam independentes e normais com média zero
e variância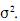 
Acerca desse modelo, julgue os seguintes itens.
O modelo descrito considera que os dados são heterocedásticos.
Considere que a população de determinado país, no instante inicial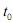
= 0, seja igual a 
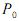> 0, que essa população cresça à taxa anual de
2% e que as taxas de imigração e de emigração sejam desprezíveis.
Com base nessas informações, julgue os próximos itens.
É possível inferir que a taxa de fecundidade nesse país é estritamente inferior a 2.
Com relação aos testes de hipóteses paramétricos, julgue os itens
subsecutivos.
No teste qui-quadrado para aderência, a estatística de teste baseia-se na comparação entre o número observado e o número esperado de elementos em cada categoria. Nesse caso, sob a hipótese nula, a estatística desse teste segue aproximadamente uma distribuição qui-quadrado, desde que o número esperado de elementos em cada categoria seja suficientemente grande.
Estão em uma sala quatro pessoas que foram convocadas
por um juiz: duas delas efetivamente testemunharão; as outras se
recusarão a testemunhar acerca de determinado fato. O juiz chamará
essas pessoas, uma a uma, para outra sala, mediante sorteio
aleatório. Considere que X seja a variável aleatória que indica o
número de pessoas chamadas até se encontrar a primeira pessoa
disposta a testemunhar.
Com base nessa situação hipotética, julgue os itens que se seguem.
Se Y for a variável que denota o número de pessoas chamadas até que a segunda pessoa disposta a testemunhar seja encontrada, então P(Y = y) = P(X = 5 - y), em que y = 1, 2, 3, 4.
Certo tipo de processo que entra num tribunal do trabalho passa por três etapas de análise, antes de ser despachado. Os tempos de cada etapa de análise são variáveis aleatórias independentes, normalmente distribuídas, com média e variância dadas na tabela abaixo.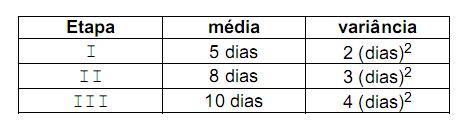 
Os processos, do tipo acima citado, que levam mais do que 26 dias para serem despachados correspondem à porcentagem de
Considere o modelo de séries temporais dado por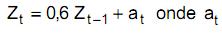 
é o ruído branco de média zero e variância 4.
Nessas condições, a variância d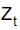e 
é
Em uma repartição pública, deseja-se saber se o número de processos autuados por dia útil, em uma semana, depende do dia da semana. Observando então o número de processos autuados nesta semana, obteve-se o quadro abaixo. 
Para concluir se o número de processos autuados depende do dia da semana, a um determinado nível de significância, utilizou- se o teste qui-quadrado. Se o número esperado de processos autuados por dia útil é igual a 16, então o valor do qui-quadrado observado para ser comparado com o correspondente qui-quadrado tabelado é
O intervalo de confiança [48,975; 51,025], com um nível de confiança de 96%, corresponde a um intervalo para a média µ' de uma população normalmente distribuída, tamanho infinito e variância populacional igual a 16. Este intervalo foi obtido com base em uma amostra aleatória de tamanho 64. Deseja-se obter um intervalo de confiança de 96% para a média µ' de uma outra população normalmente distribuída, tamanho infinito e variância populacional igual a 64. Uma amostra aleatória desta população de tamanho 400 fornecerá um intervalo de confiança com amplitude igual a
Considere que a quantidade de processos que chegam a um
auditor diariamente siga uma distribuição de Poisson, com
parâmetro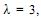 
e que cada processo, independentemente dos
demais, tenha probabilidade 0,2 de incorrer em algum tipo de
irregularidade. Com base nessa situação, julgue os itens que se
seguem.
Em face dessa situação, é correto afirmar que o número esperado de processos com irregularidade que o auditor recebe a cada dia é igual a 0,5.
Os estimadores E' =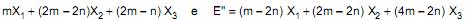 
são 2 estimadores justos utilizados para a média µ de uma população normal. 
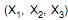corresponde a uma amostra aleatória de tamanho 3 desta população e m e n são parâmetros pertencentes aos números reais. O valor de (m + n) é igual a
